Ректификация. Экстракция из растворов. Хемосорбция, страница 3

Основные уравнения процесса. В соответствии с правилом фаз при экстракции одним растворителем Ф=2 и число параметров, характеризующих состояние системы, равно числу ее компонентов, т. е. как и при абсорбции, С = К = 3. При экстракции двумя экстрагентами (фракционная экстракция) число фаз Ф > 2, а К. ³ 4.

Уравнение линии равновесия будет:

  (p = const; t = const)

Для идеальных систем это уравнение имеет вид

где c^*_G — равновесные концентрации распределяемого вещества в экстракте и рафинате; т — коэффициент распределения.

Рис. 1-20. Основные переменные процесса экстракции а — входные переменные; б — выходные переменные; в — переменные, определяющие условия протекания процесса

Для сильно разбавленных растворов, когда концентрация органических веществ не превышает 0,1 моль/л, а концентрация неорганических — 0,01 моль/л, систему можно считать близкой к идеальной и для Р, t = const принимать коэффициент распределения т величиной постоянной.

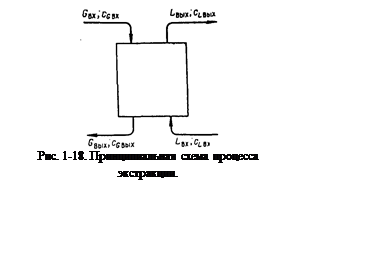
Уравнение рабочей линии. Если взаимной растворимостью исходного растворителя и экстрагента можно пренебречь, то уравнение материального баланса будет

а уравнение рабочей линии запишется следующим образом:

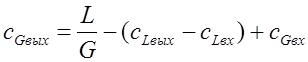
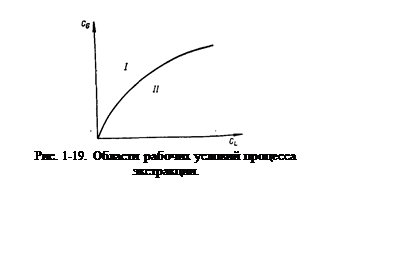
Области рабочих условий процесса изображены на рис. 1-19. Если рабочая линия находится в области I, то массоперенос направлен из фазы G в фазу L, если в области II — направление массопереноса обратное.

Уравнения скорости для процесса экстракции аналогичны кинетическим уравнениям для процесса абсорбции [см. выражения (1,81) — (1,89)].

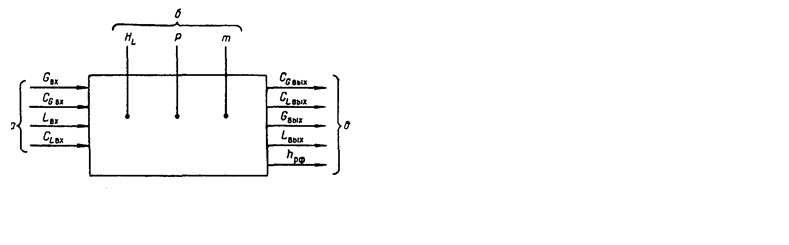
Составим математическую модель процесса применительно к экстракции в насадочном аппарате. Основные параметры процесса показаны на рис. 1-20. Кроме принятых обозначений, на этом рисунке Н_L. — удерживающая способность экстрактора по легкой фазе, h_рф — положение уровня раздела фаз относительно насадки.

Статическая модель процесса

Гидродинамические основы процесса, как обычно, включают модель потоков и гидродинамический режим.

Модели потоков. Тип модели устанавливается в зависимости от внутренней структуры потоков, отвечающей заданному гидродинамическому режиму.

Гидродинамический режим определяет основные параметры модели процесса, в том числе направление и скорость потоков в колонне, удерживающую способность, а также скорость массообмена через границу раздела фаз. Пределы существования различных гидродинамических режимов: W_Д/W_З<0.15 — область свободного движения капель; W_Д/W_З » 0.15 ¸ 1 —область стесненного движения капель.

Уравнение скорости в точке захлебывания будет:

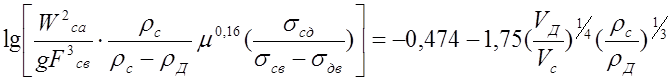
Удерживающую способность насадочного экстрактора для различных нагрузок можно приближенно рассчитывать по следующему уравнению:

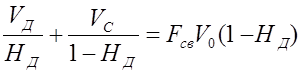
В приведенных выражениях обозначены: W_З— предельная скорость дисперсной фазы, соответствующая началу режима захлебывания; W_Д ,W_С — скорости сплошной и дисперсной фаз, рассчитанные на полное сечение колонны; а — удельная поверхность контакта фаз; F_св — свободное сечение колонны; r_С, r_Д — плотности фаз;

s_сд — граничное натяжение между фазами; s_свs_дв — поверхностные натяжения на границе каждой фазы с воздухом; V_С, V_Д — объемные расходы фаз; Н_Д — удерживающая способность колонны по дисперсной фазе; V₀ — средняя скорость всплывания капель дисперсной фазы внутри насадки при неподвижной сплошной фазе, V_С= 0 и V_Д,® 0 (находится экспериментально).

Статические характеристики. Согласно модели идеального вытеснения, имеем:

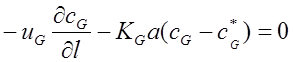
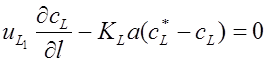
В соответствии с диффузионной моделью находим:

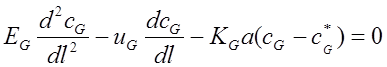
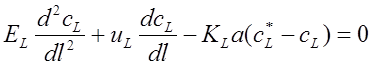
В формулах (1.154) – (1.157), как и ранее, приняты следующие обозначения:u_Gu_L - линейные скорости фаз;K_Ga, K_La, E_G, E_L - объемные коэффициенты массопередачи и коэффициенты продольного перемешивания по фазам, l - длина (высота) зоны контакта.

При расчетах принимается, что коэффициенты массопередачи по высоте колонны постоянны, а линейные скорости потоков и коэффициенты продольного перемешивания не изменяются по высоте и сечению аппарата.