Динамическая модель процесса
Динамические характеристики, или уравнения связи между основными переменными процесса во времени, будут следующие. Согласно модели идеального вытеснения, имеем:
укрепляющая часть колонны
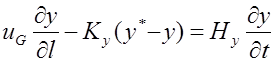
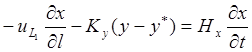
исчерпывающая часть колонны
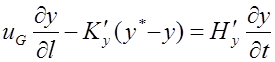
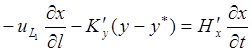
В соответствии с моделью, учитывающей продольное перемешивание, находим:
укрепляющая часть колонны
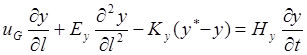
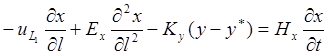
исчерпывающая часть колонны
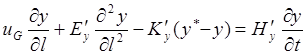
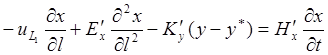
В уравнениях (1,131)—(1,138) обозначены: Ну,Hx, Н’у, Н’х — удерживающая способность насадки по пару и жидкости в обеих частях колонны.
В химической промышленности большинство разделяемых смесей состоит более чем из двух компонентов. Однако иногда смеси содержат главным образом два компонента, а концентрации остальных компонентов очень малы по сравнению с содержанием двух основных. Поэтому подобные смеси можно рассматривать как псевдобинарные, состоящие из легких и тяжелых компонентов. На таком допущении и построены наши рассуждения в данном разделе и в главе IV.
Пусть необходимо составить математическое описание процесса разделения многокомпонентной смеси, которую условно можно считать псевдобинарной смесью. Для этого введем так называемые обобщенные компоненты и обозначим концентрацию более летучего из них через xл, а концентрацию менее летучего — через xм, т. е.
xм + xл=1 и xм=1- xл
Примем, что данная многокомпонентная смесь содержит четыре компонента (z1 –z4), концентрации которых будут х1—х4. Предположим теперь, что xЛ = x1, а xм = x2 + x3 + x4. Тогда, аналогично выражению (1,122), уравнение для кривой равновесия псевдобинарной смеси имеет следующий вид:
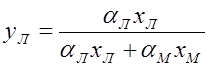
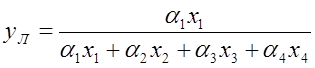
Здесь aЛ, aМ — условные относительные летучести легкого и тяжелого обобщенных компонентов; a1¸a4 относительные летучести компонентов z1 –z4. Величины aЛ и aМ соответственно равны:
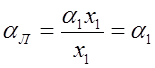
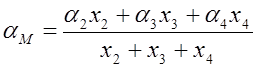
Если смесь состоит из п легколетучих компонентов и из m труднолетучих компонентов, то выражения (1,142) и (1,143) принимают вид
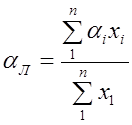
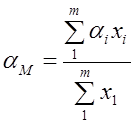
Отсюда уравнение для линии равновесия псевдобинарной смеси будет:
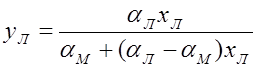
Положив xЛ = x и yЛ = y1 в уравнении (1,146), получим выражение, аналогичное формуле (1,122).
Оптимизация процесса
В качестве критерия оптимальности процесса ректификации смеси может быть выбрана разделительная способность колонны, оцениваемая по уравнению Фенске:
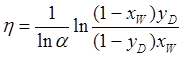
в котором уD — состав дистиллята в паровой фазе.
Средствами для достижения максимального значения h служат:
1) выбор гидродинамического режима, обеспечивающего наиболее интенсивный межфазный массообмен (режим эмульгирования); 2) выбор оптимального места ввода питания в колонну.
Экономический оптимум определяется с учетом энергетических, эксплуатационных и капитальных затрат на получение единицы продукции.
Экстракция в системах жидкость — жидкость представляет собой диффузионный процесс, протекающий с участием двух взаимно нерастворимых или ограниченно растворимых жидких фаз, между которыми распределяется экстрагируемое вещество (или несколько веществ). Разделение жидкой смеси методом экстракции включает следующие стадии: смешение исходного раствора с избирательным растворителем (экстрагентом) для создания между ними тесного контакта; разделение двух полученных несмешивающихся фаз — экстракта (раствора извлеченных веществ в экстрагенте) и рафината (остаточного исходного раствора); извлечение целевых продуктов из экстракта и регенерацию экстрагента из экстракта и рафината.
Процессы жидкостной экстракции широко распространены в химической технологии. Они эффективно используются для выделения в чистом виде различных продуктов органического и нефтехимического синтеза, извлечения и разделения редких и рассеянных элементов, очистки сточных вод и т. д.
Принципиальная схема процесса экстракции из растворов показана на рис. 1-18. На схеме приняты обозначения: G,cG — расход тяжелой фазы и концентрация в ней компонента соответственно на входе в экстрактор и выходе из него; L,cL — то же, для легкой фазы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.