Сглаживание экспериментальных переходных функций

Лабораторная работа 3.

Сглаживание экспериментальных переходных функций.

Цель работы: рассмотреть методы сглаживания экспериментальных переходных функций.

Сглаживание переходных функций четвертыми разностями представляет собой аппроксимацию каждых 5 соседних значений функции Z(i) параболой второго порядка с помощью метода наименьших квадратов. При этом вычисляется только разность (поправка) между параболой и значением средней из 5 ординат Z(i). Потом осуществляется сдвиг вправо на один номер i и опять вычисляется поправка для значения Z(i+1). Значение этой поправки пропорционально:

Где i=2,3,….,n-2.

Значение оценки переходной функции h(i) рассчитывается по формуле:

Чтобы избежать исчезновения 4 значений h(i) при  i=0,1,n-1,n необходимо использовать следующие формулы:

где  - центральная 3 разность:

Пишем программу:

clc,clear

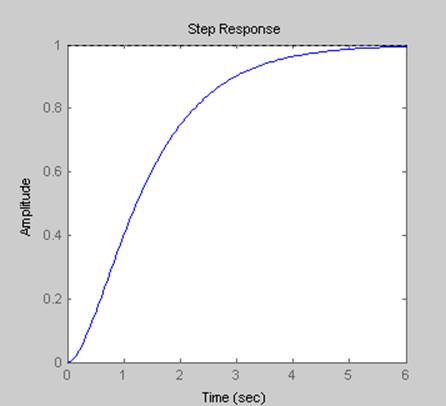
w=tf([1],[0.5 1.5 1])

step(w)

[Y T]=step(w)

% определяем число значений

[n m]=size(Y)

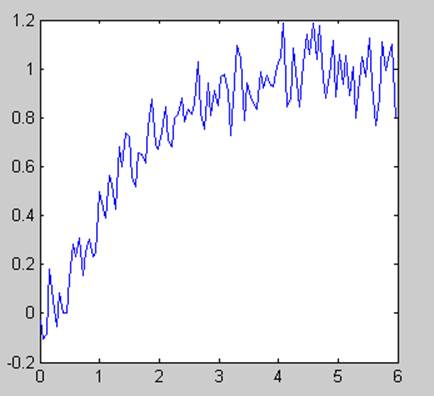
%wwedem sluczajnyj proces

f=0.1*normrnd(0.1,1,n,m)

% зашумленный сигнал H

z=Y+f

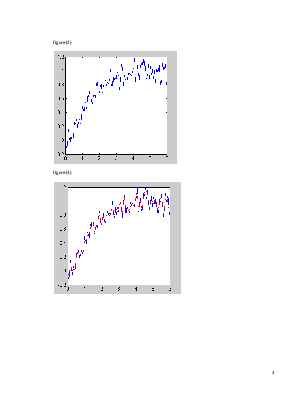
figure(2)

plot(T,z)

% метод 3-x и 4-x разностей

for i=3:n-2

d4z(i)=z(i-2)-4*z(i-1)+6*z(i)-4*z(i+1)+z(i+2)

h(i)=z(i)-d4z(i)/12

end

d3z=z(1)-3*z(2)+3*z(3)-z(4)

h(1)=z(1)-1/5*d3z+1/12*d4z(3)

h(2)=z(2)+2/5*d3z-1/7*d4z(3)

d3z2=z(n-3)-3*z(n-2)+3*z(n-1)-z(n)

h(n)=z(n)+1/5*d3z2-1/12*d4z(n-2)

h(n-1)=z(n-1)-2/5*d3z2+1/7*d4z(n-2)

figure(3)

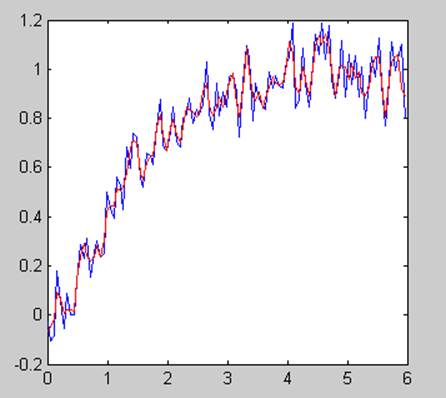
plot(T,z,'b',T,h,'r')

Получаем результаты:

T-вектор значения времени (109×1),

Y- вектор значения функции (109×1),

d3z=-0.14486,

d3z2=0.37021,

dz4=(1×107),

figure(1)

figure(2)

figure(3)