Планы 2-го порядка. Вычислительный алгоритм ортогональных планов 2-го порядка

20. Планы 2-го порядка

Дана исходная таблица плана:

N							y
1	+1	–1	–1	+1	+1	+1
2	+1	+1	–1	–1	+1	+1
3	+1	–1	+1	–1	+1	+1
4	+1	+1	+1	+1	+1	+1
5	+1	+a	0	0	a2	0
6	+1	–a	0	0	a2	0
7	+1	0	+a	0	0	a2
8	+1	0	–a	0	0	a2
9	+1	0	0	0	0	0

Для приведения таблицы к ортогональному виду применяется замена квадратичных столбцов линейными по следующим соотношениям:

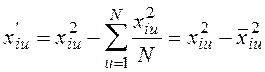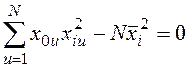;  ;   но .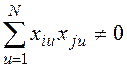

Окончательно матрица приводится к ортогональному виду величиной выбора звёздного плеча a, при этом a зависит от числа переменных n. Это достигается получением в обратной матрице  недиагональных элементов =0.

n 2 3 4 5 a 1,0 1,216 1,415 1,576

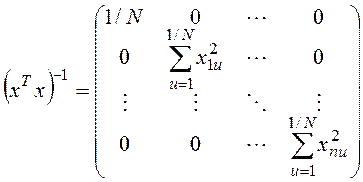       и тогда получим ортогон. м-цу данного плана

Для полностью ортогональной м-цы плана a будет равно:

Построим ортогональный план 2-го порядка для примера:

получить ур-е некоторго вида для объекта . N=2²+2×2+1=9.

Вместо квадратичных столбцов матрицы введём (было ).

N							y
1	+1	–1	–1	+1	1/3	1/3
2	+1	+1	–1	–1	1/3	1/3
3	+1	–1	+1	–1	1/3	1/3
4	+1	+1	+1	+1	1/3	1/3
5	+1	+1	0	0	1/3	–2/3
6	+1	–1	0	0	1/3	–2/3
7	+1	0	+1	0	–2/3	1/3
8	+1	0	–1	0	–2/3	1/3
9	+1	0	0	0	–2/3	–2/3

Теперь можно перевести в натуральные величины: 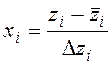, поставить эксперимент и определить .

По результатам данного эксперимента м. получить ур-е след. вида:

.

Коэф-ты определяются методом наименьших квадратов:

.

;                ;                ;            .

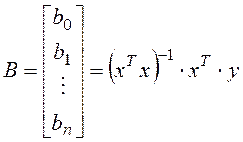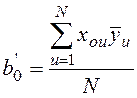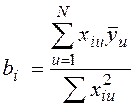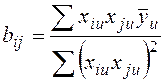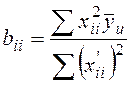n=2:  .

Определим :  .

Тогда .

Вычислительный алгоритм ортогональных планов 2-го порядка аналогичен соответствующему алгоритму для планов 1-го порядка, т.е. оценку воспроизводимости опытов проводят аналогично как и для ПФЭ, оценка значимости коэф-тов полученного ур-я:

Критерий Стьюдента: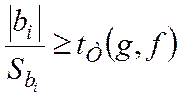

;                ;                    .

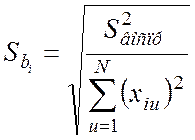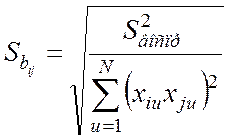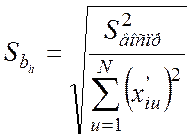В планах 2-го порядка в отличие от планов 1-го порядка оценка коэф-тов ур-я производится с различной точностью.