Идентификация статических моделей методом пассивного эксперимента

Лабораторная работа  5.

Идентификация статических моделей методом пассивного эксперимента.

Цель работы: рассмотреть основные этапы процедуры идентификации моделей методами пассивного эксперимента, определить коэффициенты модели, определить значимость коэффициентов уравнения и адекватность модели.

Процедура идентификации моделей методами пассивного эксперимента составляется из 3 основных этапов:

Ø  Определение коэффициентов статической модели методам наименьших квадратов;

Ø  Оценка значимости коэффициентов модели;

Ø  Оценка адекватности модели экспериментальным данным.

Для нахождения коэффициентов модели чаще всего используют метод наименьших квадратов:

Вторым этапом  идентификации регрессионной модели объекта является оценка значимости ее коэффициентов . Проверка гипотезы о значимости проводится по критерию Стьюдента в случае проведения активного эксперимента.

Третьим этапом идентификации регрессионной модели является проверка адекватности мат. описания. Мерой разброса данных является остаточная дисперсия:

Пишем программу:

clc, clear

% эксперементал. данные

x=[0.3;1.2;2;3;4.2;5]

y1=[8.2;28;43.1;49.3;52;56.5]

y2=[12.3;32;47.2;51.4;53;57.4]

n=length(x) – Нахождение числа объектов

y=(y1+y2)/2

k=corrcoef(x,y)

% р.модель

X=[ones(n,1) x]

A=((X'*X)^(-1))*(X')*y;

z=0.3:0.1:5;

Y=A(1)+A(2)*z;

figure(1)

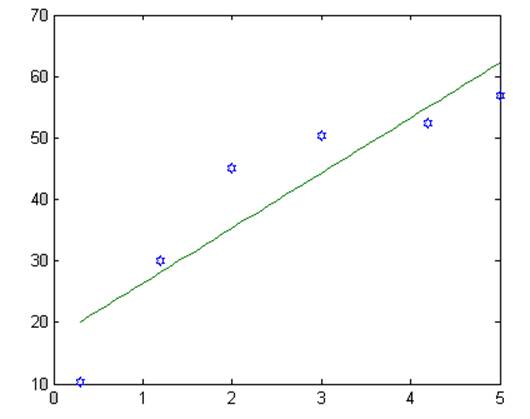
plot(x,y,'h',z,Y) – Вывод первый порядок не подходит , берем второй

% второй порядок

X2=[ones(n,1) x x.^2];

A=((X2'*X2)^(-1))*(X2')*y;

z=0.3:0.1:5;

Y2=A(1)+A(2)*z+A(3)*z.^2;

figure(2)

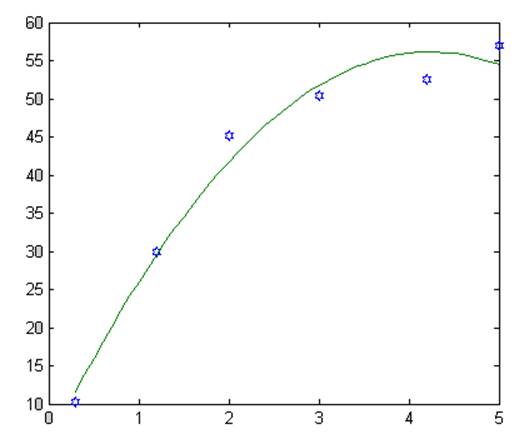
plot(x,y,'h',z,Y2)

% третий порядок

X3=[ones(n,1) x x.^2 x.^3];

A=((X3'*X3)^(-1))*(X3')*y;

z=0.3:0.1:5;

Y3=A(1)+A(2)*z+A(3)*z.^2+A(4)*z.^3;

figure(3)

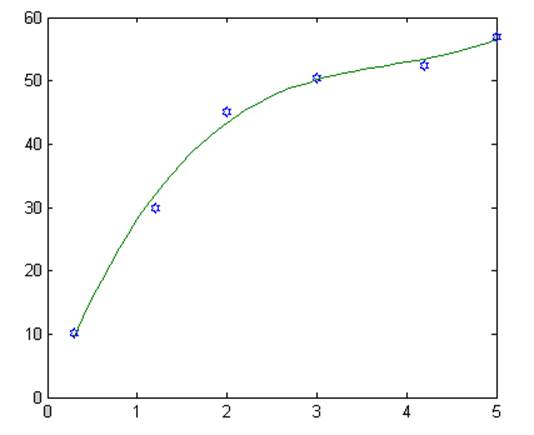
plot(x,y,'h',z,Y3)

% проверка значимости

m=2;

f=n*(m-1); - степень свободы

p=0.95; - доверительный интервал

tt=tinv(p,f); - табличное значение

%C(i)=diag((X3'*X3)^(-1))

Dy=cov(y)

u=length(A) – число коэффициентов регрессионной модели

for i=1:u

C=diag((X3'*X3)^(-1))

tr(i)=abs(A(i))/sqrt(C(i)*Dy) – расчетное значение

end

% проверка адекватности

f1=n-1

f2=n-u

fish=finv(p,f1,f2)

Dost=(y-X3*A)'*(y-X3*A)/(n-u) – остаточная дисперсия

Dv=((y1-y).^2+(y2-y).^2)

Dvv=sum(Dv)/f1

D=Dost/Dvv

Получаем:

figure(1) – первый порядок

figure(2) – второй порядок

figure(3) – третий порядок

n=6

k=0.91

u=4

tr=0.0237  0.7853  0.4203

fish=19.2964

Dost=4.3349

Dv=8.4050 8.0000 8.4050 2.2050 0.5000 0.4050

Dvv=5.5840

D=0.7763

Вывод : табличное значение критерия Стьюдента больше расчетного отсюда следует, что все коэффициенты незначимые .Т.к. самый маленький в tr это 1-й то уберем эту часть в модели.

Т.к. D=0.7763 меньше fish=19.2964 – то для третьего порядка получаем адекватную модель.