














Предел функции. Непрерывная функция
§ 10. Определения, примеры и свойства предела функции
Пусть ЕÌR , и пусть а – предельная точка множества Е. Пусть f: E®R, (или y=f(x)).
Определение
1. (по Коши). Число А называется пределом функции f(x) при x стремящемся к
а, если "e>0 $d=d(e, a)>0 такое, что "xÎE,
удовлетворяющих неравенству 0<|x – a|<d
выполняется |f(x) – A|<e.
Обозначение ![]() .
.
Проколотой
окрестностью точки называется окрестность точки, из которой удалена сама точка.
Если ![]() окрестность точки а, то проколотую
окрестность обозначают
окрестность точки а, то проколотую
окрестность обозначают ![]() . Кроме того будем обозначать
. Кроме того будем обозначать ![]() . Если а – предельная точка множества Е, то
. Если а – предельная точка множества Е, то
![]() – не пусто.
– не пусто.
Определение
1¢. Число А называется
пределом функции f(x) при x®a, если ![]() .
.
Пример. f(x) = x sin(1/x) при x®0.
Определение 2. (по Гейне). Число А называется пределом функции f(x) при x стремящемся к а, если для любой последовательности {xn} точек xnÎE\{a}, сходящейся к а, соответствующая последовательность значений функции {f(xn)} сходится к А.
Теорема 10.1. Определения предела функции по Коши и по Гейне эквивалентны.
Доказательство: очевидно (самостоятельно).
Определение
3. Число А называется правым (левым) пределом функции f(x) в
точке а, если "e>0 $d=d(e, a)>0 такое, что "xÎE,
удовлетворяющих неравенству 0<x – a<d
(0<а – x<d) выполняется |f(x) –
A|<e. Обозначение ![]() .
.
Теорема 10.2. Функция f(x) имеет предел при x®a тогда и только тогда, когда в точке а существуют левый и правый пределы, равные между собой.
Доказательство: очевидно (самостоятельно).
Определение
4. Число ![]() , если "e>0 $d=d(e)>0
такое, что "xÎE, удовлетворяющих неравенству |x|>d выполняется |f(x) – A|<e.
, если "e>0 $d=d(e)>0
такое, что "xÎE, удовлетворяющих неравенству |x|>d выполняется |f(x) – A|<e.
Замечание:
Если ![]() , то
, то ![]() .
.
Теорема
10.3. (Арифметические свойства предела). Пусть f: E®R и g: E®R.
Если существует ![]() и
и ![]() , то а).
, то а). ![]()
б).![]()
в).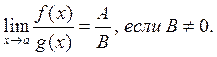
г). f(x) ограничена в некоторой окрестности точки а.
Доказательство основывается на определении предела по Гейне и арифметических свойствах предела последовательности (самостоятельно).
Пример.
Предел рациональной функции 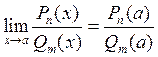 ,
, ![]() .
.
Теорема
10.4. (Предельный переход в неравенствах) а). Пусть f: E®R и g: E®R. Если существует ![]() и
и ![]() , причем А<B, то $
, причем А<B, то $![]() , что f(x)<g(x) "xÎ
, что f(x)<g(x) "xÎ![]() .
.
б). Если для
f,g,h: E®R выполняется f(x)£g(x)£h(x)
и ![]() , то существует
, то существует ![]() .
.
Доказательство:
а). Пусть С таково, что А<C<B. Из определения предела следует, что для e=С-А $d1>0, что для x,
удовлетворяющих 0<|x – a|<d1
выполняется |f(x) – A|<C-A, т.е. 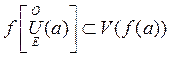 . Аналогично, для e=B-C>0 $d2>0, что для x, удовлетворяющих
0<|x – a|<d2
выполняется |g(x) – B|<B-C, т.е. B-(B-C)=C<g(x). Обозначим d=min(d1,d2),
тогда для x, удовлетворяющих неравенству 0<|x – a|<d одновременно выполняется f(x)<C<g(x),
таким образом,
. Аналогично, для e=B-C>0 $d2>0, что для x, удовлетворяющих
0<|x – a|<d2
выполняется |g(x) – B|<B-C, т.е. B-(B-C)=C<g(x). Обозначим d=min(d1,d2),
тогда для x, удовлетворяющих неравенству 0<|x – a|<d одновременно выполняется f(x)<C<g(x),
таким образом, ![]() = {xÎÎЕ/0<|x – a|<d}.
= {xÎÎЕ/0<|x – a|<d}.
б). Очевидно.
Следствие.
Пусть ![]() и
и ![]() , если
в некоторой
, если
в некоторой ![]() выполняется
выполняется
1. f(x)>g(x), то А³В;
2. f(x)³g(x) , то А³В.
§ 11 Вопросы существования предела функции
Пусть f: X®Y и g: Y®R. Определим сложную функцию h:X® R по правилу h=g°f, т.е. h(x)=g(f(x)).
Теорема
11.1. Пусть ![]() , причем f(x)¹y0 при x¹x0. Пусть, кроме того, существует
, причем f(x)¹y0 при x¹x0. Пусть, кроме того, существует ![]() , тогда существует
, тогда существует ![]() .
.
Доказательство:
Используем Определение 1¢
предела функции. Пусть ![]() – произвольная окрестность точки
А. По условию теоремы существует
– произвольная окрестность точки
А. По условию теоремы существует ![]() . Однако для данной
окрестности
. Однако для данной
окрестности ![]() , в силу существования предела функции f(x) найдется такая окрестность
, в силу существования предела функции f(x) найдется такая окрестность ![]() ,
, ![]() . Тогда
. Тогда
![]() , т.е. А является пределом h(x) при x®x0.
, т.е. А является пределом h(x) при x®x0.
Замечание. Данную теорему называют также правилом замены переменной под знаком предела.
11.2. Критерий Коши
Теорема
11.2. Функция ![]() имеет предел в точке
имеет предел в точке ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() , что
, что ![]() ,
удовлетворяющих условиям
,
удовлетворяющих условиям ![]() ,
, ![]() справедливо:
справедливо: ![]() (условие
Коши).
(условие
Коши).
Доказательство.
1)
Необходимость. Пусть ![]() . Фиксируем
. Фиксируем ![]() . В силу определения 1 § 1
. В силу определения 1 § 1 ![]() , что если
, что если ![]() и
и ![]() , то
, то  и
и 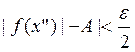 , тогда
, тогда ![]() .
.
2) Достаточность.
Пусть ![]() удовлетворяет условию Коши в точке
удовлетворяет условию Коши в точке ![]() , покажем наличие предела. Пусть
, покажем наличие предела. Пусть ![]() – произвольная последовательность из
– произвольная последовательность из ![]() сходящаяся к
сходящаяся к ![]() .
Согласно определению 3 предела по Гейне, достаточно доказать, что: а)
соответствующая последовательность
.
Согласно определению 3 предела по Гейне, достаточно доказать, что: а)
соответствующая последовательность ![]() сходится к некоторому
числу
сходится к некоторому
числу ![]() ; б) это число одно и тоже для всех сходящихся
к
; б) это число одно и тоже для всех сходящихся
к ![]() последовательностей
последовательностей ![]() .
.
а) Фиксируем ![]() согласно условию Коши
согласно условию Коши ![]() так как
так как ![]() –
сходится к
–
сходится к ![]() , то по этому
, то по этому ![]() , что
, что ![]()
![]() и
и ![]()
![]() , но тогда по условию
Коши
, но тогда по условию
Коши ![]()
![]() ,
, ![]() . Это означает фундаментальность
последовательности
. Это означает фундаментальность
последовательности ![]() и, следовательно, в силу
критерия Коши Т.1 §2 гл.3 последовательность
и, следовательно, в силу
критерия Коши Т.1 §2 гл.3 последовательность ![]() сходится
к некоторому числу
сходится
к некоторому числу ![]() .
.
б) Покажем,
что ![]() не зависит от выбора последовательности
не зависит от выбора последовательности ![]() сходящейся к
сходящейся к ![]()
![]() .
.
Пусть ![]() также сходится к
также сходится к ![]() ,
но
,
но ![]() . Рассмотрим последовательность
. Рассмотрим последовательность ![]() – эта последовательность также сходится к
– эта последовательность также сходится к ![]() . По ранее доказанному последовательность
. По ранее доказанному последовательность ![]() обязана сходиться к некоторому пределу
обязана сходиться к некоторому пределу ![]() . Но тогда и любая ее подпоследовательность
обязана сходиться к этому же пределу. Итак, подпоследовательность с нечетным
номером сходится к
. Но тогда и любая ее подпоследовательность
обязана сходиться к этому же пределу. Итак, подпоследовательность с нечетным
номером сходится к ![]() , а с четными к
, а с четными к ![]() . Следовательно,
. Следовательно, ![]() .
Теорема доказана.
.
Теорема доказана.
Определение
2. Функция ![]() называется ограниченной
(ограниченной сверху, ограниченной снизу), если
называется ограниченной
(ограниченной сверху, ограниченной снизу), если ![]() , что
, что ![]() выполняется
выполняется ![]() (
(![]()
![]() ).
).
Определение
3. Функция ![]()
![]() называется
называется
-
возрастающей на ![]() , если
, если ![]() ,
,
-
неубывающей ![]() ,
,
-
невозрастающей ![]() ,
,
-
убывающей на ![]()
![]() .
.
Функции перечисленных типов называются монотонными.
§ 12. Два замечательных предела
п. 1. Первый замечательный предел
Теорема
12.1. 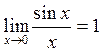 .
.
![]() – ордината точки, в которую переходит
точка (1,0) при повороте на угол
– ордината точки, в которую переходит
точка (1,0) при повороте на угол ![]() радиуса.
радиуса.
1) докажем,
что 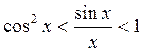 при
при 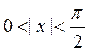 . Так
как
. Так
как ![]() и
и ![]() –
четные формулы, то достаточно рассмотреть
–
четные формулы, то достаточно рассмотреть 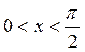 .
.
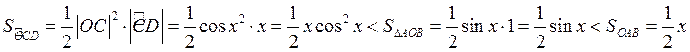 .
.
Итак, 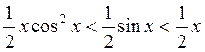
![]()
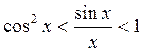 .
.
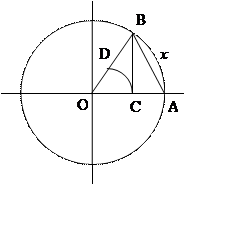 .
.
2) ![]() (причем равенство возможно только при
(причем равенство возможно только при ![]() .
.
![]()
Действительно,
для 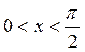 2) следует из 1), а для
2) следует из 1), а для 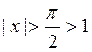 , также получаем
, также получаем ![]() .
.
3) ![]() , т.к.
, т.к. ![]() и
и ![]() .
.
4)  , т.к.
, т.к.  , для
, для 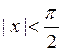 .
.
п. 2.
Теорема 12.2.  .
.
Доказательство.
Рассмотрим ![]() – целая часть наибольшее целое число, не
превосходящее
– целая часть наибольшее целое число, не
превосходящее ![]() .
. ![]() ,
очевидно
,
очевидно ![]() , если
, если ![]()
![]() .
.
Вспомним, что
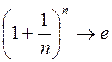 .
.
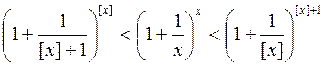
![]()
т.е. 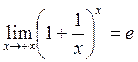 .
.
Аналогично 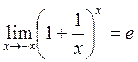 .
.

Замена ![]() приводит к
приводит к ![]() .
.
§ 13. Сравнение асимптотического поведения функций
Когда возникает вопрос об описании поведения функции вблизи некоторой точки (или бесконечности), в которой, как правило, сама функция не определена, то говорят что интересуются асимптотикой или асимптотическим поведением функции в окрестности этой точки. Асимптотическое поведение функции характеризуют обычно с помощью более простой или более изученной функции, которая в окрестности исследуемой точки с достаточно малой погрешностью воспроизводит значения изучаемой функции.
Так как ![]() при
при ![]() ведет
себя как 1.
ведет
себя как 1.  при
при ![]() как
как ![]() , а при
, а при ![]() как
как ![]() ,
, ![]() как
как ![]() .
.
Определение
1. Функция ![]() называется бесконечно малой в
точке
называется бесконечно малой в
точке ![]() , если
, если ![]() .
.
Заметим, что
если ![]() , то
, то ![]() бесконечно
малая и
бесконечно
малая и ![]() .
.
Определение
2. Говорят, что функция ![]() есть бесконечно малая
по сравнению с функцией
есть бесконечно малая
по сравнению с функцией ![]() в точке
в точке ![]() и пишут
и пишут ![]() при
при ![]() , если в некоторой окрестности
, если в некоторой окрестности
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.