Исследование одношаговых методов численного решения задачи Коши на примере задачи о свободных и вынужденных колебаниях линейного осциллятора

Санкт-Петербургский государственный политехнический университет

Институт прикладной математики и механики

Лабораторная работа №1 по дисциплине

«Численные методы в теории колебаний»

Исследование одношаговых методов численного решения задачи Коши.

Руководитель: ________ Смирнова Н. А.

Выполнили: Студенты группы 33602/3______Абдуллаев Р. А.

Чернышев К.С.

Панюшев А. В.

Санкт-Петербург

2014

ЦЕЛЬ РАБОТЫ

Будем исследовать качество работы трех одношаговых методов численного решения задачи Коши: явный, неявный методы Эйлера и метод средней точки, на примере задачи о свободных и вынужденных колебаниях линейного осциллятора. Из-за принципиальной разницы в моделировании консервативных, слабо и сильно демпфированных систем, необходимо изучить поведение численной модели для каждой из этих систем.

Свободные колебания.

Консервативная система:

Шаг h=0.1

Вид колебаний

O - график явного метода Эйлера

X - график неявного метода Эйлера

‘-’ – метод средней точки

‘-‘ – аналитическое решение

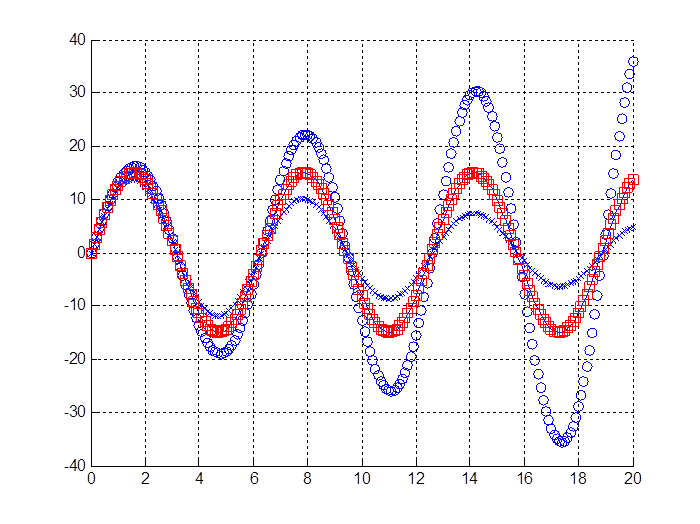
Рисунок 1 Зависимость обобщенной координаты от времени

В консервативной системе нет потери энергии, поэтому полезно построить график амплитуды(A=sqrt(E))

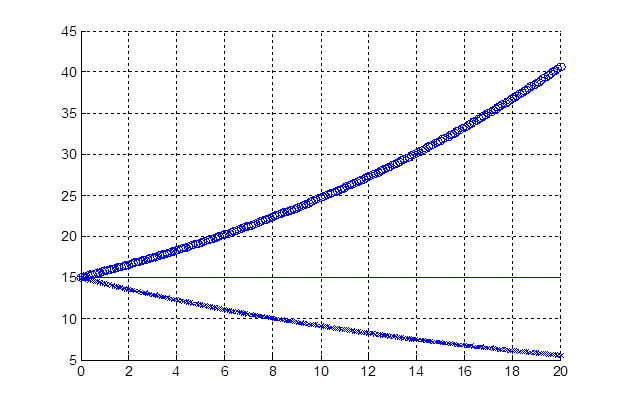
Рисунок 2 Зависимость амплитуды от времени

Видно, что с точным решением совпадает только метод средней точки. Из-за искажений при численном интегрировании, явная и неявная схемы отклоняются от решения, использовать их нельзя.

Можно также рассмотреть расположение корней hλ  относительно областей устойчивости для разных методов и их зависимость от шага: 

 

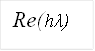
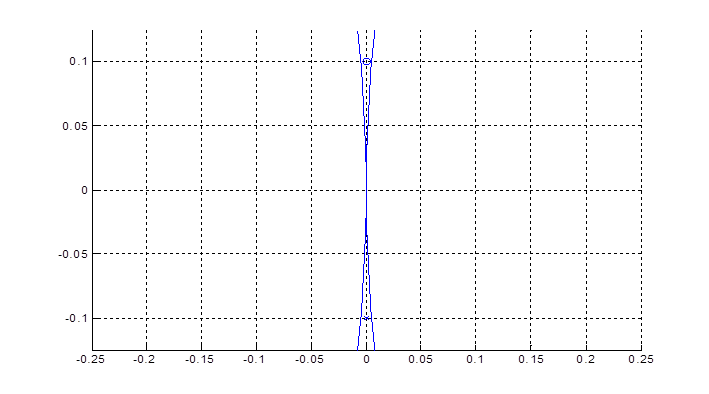
Рисунок 3 Положение корней hλ

Корни чисто мнимые, всегда попадают в границу области устойчивости метода средней точки.

Система с малым демпфированием:( v=0.05)

Системе с малым демпфированием характерны большая колебательность и малые значения hv

h=0.1

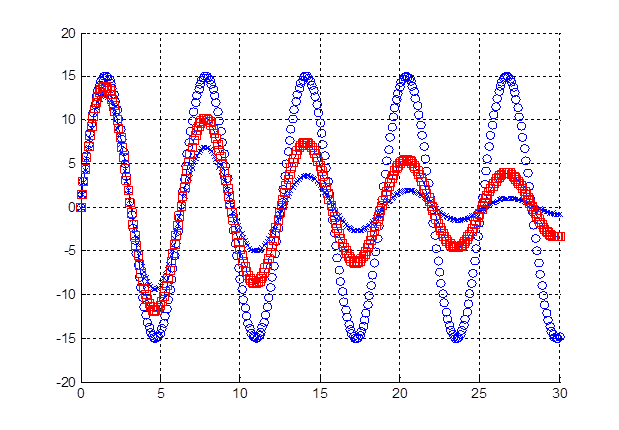
Рисунок 4  Зависимость обобщенной координаты от времени

Средняя точка почти совпадает с аналитическим решением. Неявная схема сходится. Явная схема попала на границу устойчивости.

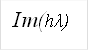
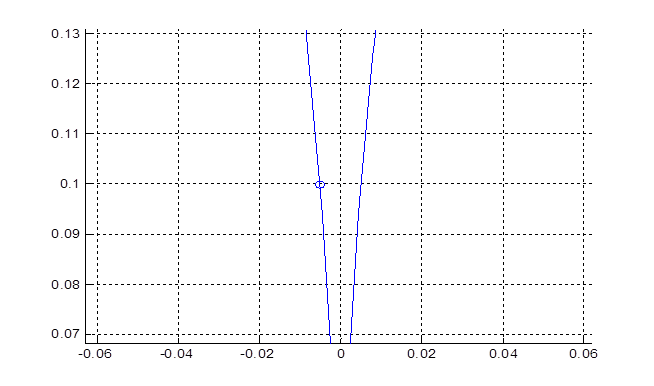
Рисунок 5 Положение корней hλ

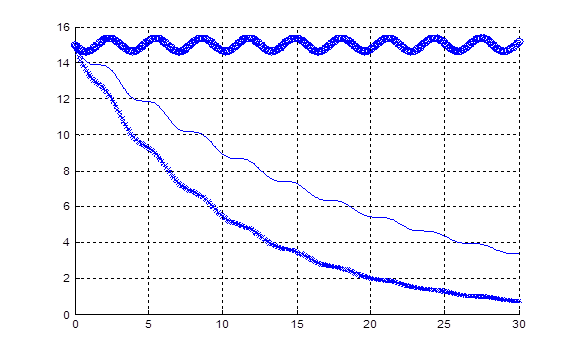
Рисунок 6 Зависимость амплитуды от времени

По расположению корней hv видно, что при небольшом увеличении величины шага или трения, явная схема начнет расходиться , поэтому использовать нужно метод средней точки или неявную схему.

Но неявная схема сходится слишком быстро, поэтому точность поведения системы с малым демпфированием лучше смотреть  по средней точке.

Большое демпфирование: (v=9)

h=0.1

Вид колебаний:

При большом демпфировании корни вещественны, и чтобы увидеть характерное поведение системы, можно рассмотреть только быструю экспоненту, то есть небольшой промежуток времени. Колебательность отсутствует.

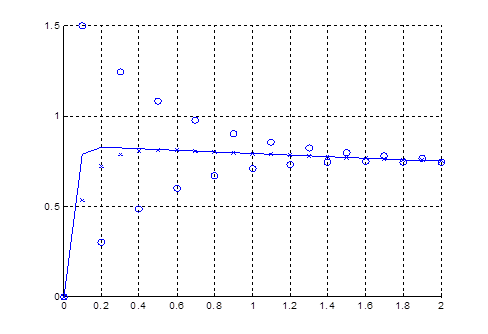
Рисунок 7 Зависимость обобщенной координаты от времени

Явная схема при таком шаге дает отрицательное значение переходному множителю, поэтому явный метод сходится пилообразно.  Неявный и метод средней точки сходятся.

h=0.2

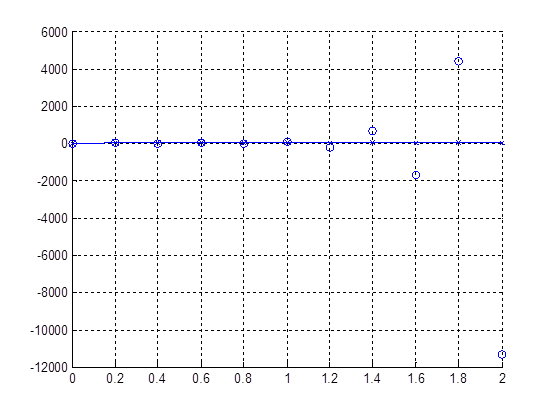
Рисунок 8 Зависимость обобщенной координаты от времени для явного метода

Явный расходится пилообразно.

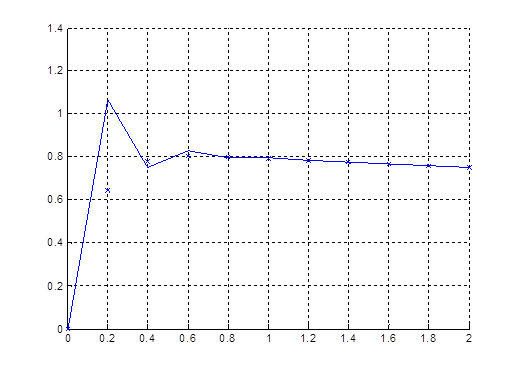
Рисунок 9 Зависимость обобщенной координаты от времени для неявного метода и метода средней точки

Метод средней точки сходится пилообразно. Неявный сходится.

Таким образом, для системы с большим демпфированием лучше использовать неявную схему, которая работает и при большом шаге интегрирования.

Вынужденные колебания:

Будем исследовать качество работы указанных выше трех алгоритмов в задаче о вынужденных колебаниях осциллятора с малым демпфированием при действии на него гармонической вынуждающей силы.

q’’+2*v*q’+q=Q*sin(wt)

v=0.05

Устойчивость рассматриваемой системы не зависит от правой части уравнения, а устойчивость различных методов для систем с малым демпфированием была рассмотрена выше. Необходимо рассмотреть, что происходит с системой в области резонанса,  снимая амплитудно-частотную характеристику (АЧХ) в зоне частот, близких к резонансу.

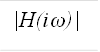Амплитудно-частотная характеристика:

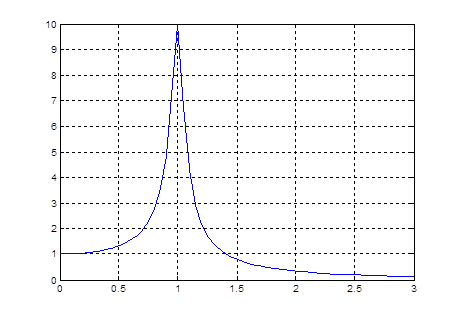
Рисунок 10 Амплитудно-частотная характеристика

Явная схема

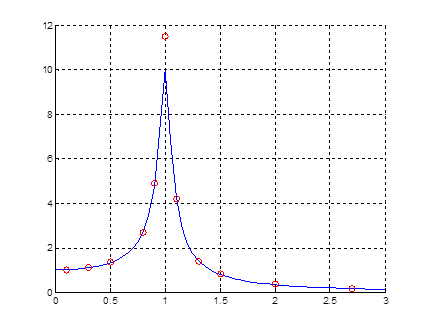
Рисунок 11 Амплитудно-частотная характеристика

Явный метод даёт хороший результат на высоких и низких частотах. Но вблизи резонансной частоты амплитуды сильно расходятся.

Неявная схема

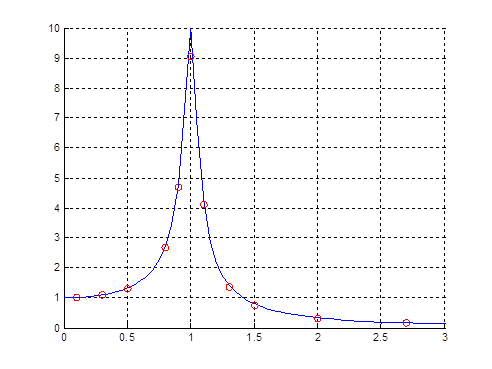
Рисунок 12 Амплитудно-частотная характеристика

Неявный метод, как и явный, допустимо использовать только для низких и высоких частот, избегая области резонанса.

Средняя точка

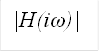
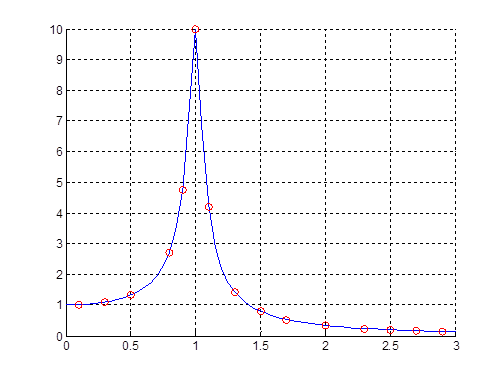
Рисунок 13 Амплитудно-частотная характеристика

Графики точного решения и приближенного практически совпадают. То есть метод средней точки можно использовать для гармонического осциллятора при малом демпфировании на всем диапазоне частот.

ВЫВОДЫ

1) При моделировании консервативных систем с точным решением совпадает метод средней точки. При чисто мнимом значении λ, корни hλ всегда будут на мнимой оси (при любом шаге), которая является границей области устойчивости точного и численного решений.

Из-за искажений при численном интегрировании, явная и неявная схемы отклоняются от решения, использовать их нельзя при любом шаге. Область устойчивости неявного включает в себя мнимую ось, а явного – нет.

2) У систем с малым демпфированием для явной схемы необходимо выбрать шаг так, чтобы попасть в область устойчивости,  а метод средней точки и неявная схема будут сходиться при любом шаге.

Но неявная схема сходится слишком быстро, поэтому точность поведения системы с малым демпфированием лучше смотреть  по средней точке.

3) В системах с большим демпфированием, получаем различные результаты в зависимости от величины . В явной схеме, переходный множитель зависящий от , может стать отрицательным (решение - быстро убывающаю экспонента в виде знакочередующейся), или большим единицы по модулю (метод расходится).

Для неявной схемы имеем, что при   переходный множитель стремится к 0, то есть устойчивость системы при любом шаге.

Метод средней точки даёт наилучшее приближение к точному решению, однако переходный множитель может быть отрицательным, в зависимости от шага.

Таким образом, для исследования жестких систем рекомендуем неявный метод Эйлера.

4) Для вынужденных колебаний получаем, что явная и неявная схемы не применимы в области резонанса. Для остальных областей методы дают хорошие результаты.

Метод средней точки лучше всего подходит для  исследования данной системы.