Проектирование несущих конструкций многоэтажных зданий, страница 9

Ширину раскрытия трещин определяем по формуле

,  (3.20)

где β – коэффициент, учитывающий отношение расчётной ширины раскрытия трещин к средней; β=1,7 – для сечений, наименьший размер которых не превышает 800мм; β=1,3 – для сечений, наименьший размер которых менее 300мм; ε_rm – среднее расстояние между трещинами, мм,

,   (3.21)

где Ø – диаметр стержня, мм, или средний диметр при нескольких диаметрах; k₁=0,8 – для стержней периодического профиля; k₂=0,5 – при изгибе; k₂=1 – при осевом растяжении; ρ_eff – эффективный коэффициент армирования,

,   (3.22)

где A_s – площадь сечения арматуры, расположенной внутри эффективной площади сечения; A_с,eff – эффективная площадь сечения растянутой зоны при высоте, равной 2,5 расстояния от наиболее растянутой грани до центра тяжести арматуры, h_eff=2,5(h-d).

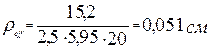
Средние деформации арматуры определяются по формуле

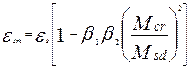   (3.23)

где ε_sm – деформация растянутой арматуры в сечении с трещиной; β₁=1 – для арматурных стержней периодического профиля; β₁=0,5 – для гладкой арматуры; β₂=1 – при кратковременном действии нагрузки; β₂=0,5 – при длительно действующей нагрузке; M_cr – изгибающий момент, при котором возникают трещины; M_sd – изгибающий момент от нормативной нагрузки.

Усилия трещинообразования определяются по упрощённой зависимости как для бетонного сечения

,   (3.24)

где W_c – момент сопротивления бетонного сечения; W_c=20·50²/6=8333,3см³. Средняя прочность бетона класса C30/34 при растяжении f_ctm=2,6Н/мм²; M_cr=2,6·8333,3/10³=21,67кН·м; M_sd=140,93кН·м.

Напряжения в арматуре при образовании трещин

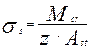    (3.25)

где z=0,85d;

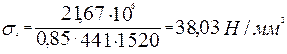
Относительная деформация арматуры

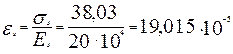
Средняя деформация растянутой арматуры

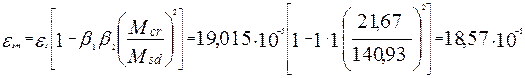
Ширина образования трещины при кратковременном действии нагрузки

При длительно действующей нормативной нагрузке

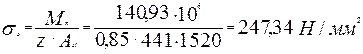
Относительная деформация растянутой арматуры

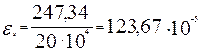
Средняя деформация растянутой арматуры

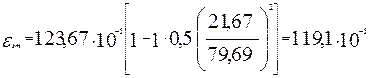
Ширина образования трещин при длительной нагрузке

Повторим все расчёты для опорного сечения. Исходные данные не изменяются средняя прочность бетона класса C30/34 при растяжении f_ctm=2,6Н/мм²; M_cr=2,6·8333,3/10³=21,67кН·м; M_sd=118,32кН·м.

Определим эффективный коэффициент армирования и среднее расстояние между трещинами:

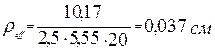
Напряжения в арматуре при образовании трещин

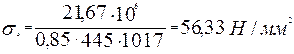
Относительная деформация арматуры

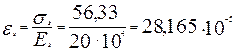
Средняя деформация растянутой арматуры

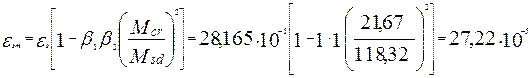
Ширина образования трещины при кратковременном действии нагрузки

При длительно действующей нормативной нагрузке

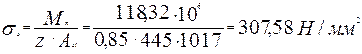
Относительная деформация растянутой арматуры

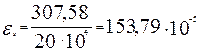
Средняя деформация растянутой арматуры

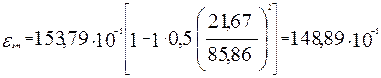
Ширина образования трещин при длительной нагрузке

3.9 Расчёт деформаций

Прогиб определяем в первом пролёте ригеля при его невыгодном загружении. Ограничение прогибов железобетонных конструкций связано с обеспечением условий нормальной эксплуатации зданий и сооружений.

Способ определения прогиба основан на сравнении коэффициента жёсткости (l_eff/d), который косвенным образом характеризует деформативность конструкции, с допустимыми значениями (l_eff/d)_lim.

Проверку прогибов производим по условию

,  (3.26)

где (l_eff/d)_lim - граничное значение коэффициента жёсткости (для крайних пролётов балок и плит, армированных в одном или двух направлениях принимают, равными: при ρ_l ≥1,5% -  (l_eff/d)_lim = 18,  при ρ_l ≤0,5% -  (l_eff/d)_lim = 26, где ρ_l=A_s/(bd)=15,2/(20·44,1)=1,72%, следовательно  (l_eff/d)_lim = 18);

Значение коэффициента δ₁:

- для балок и плит, опёртых по контуру, δ₁=1 при l_eff ≤ 7м,   δ₁ = 7/ l_eff   при  l_eff >7;

напряжение в арматуре при f_yk = 400 Н/мм² не должны превышать 250Н/мм². Если возникают большие напряжения, то вводят коэффициент

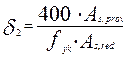     (3.27)

где A_s,prov – принятая площадь растянутой арматуры; A_s,red - требуемая  по расчёту площадь растянутой арматуры.

Вычисляем значения коэффициентов δ₁ и  δ₂  . Коэффициент  δ₁ = 1, так как пролёт ригеля составляет 5,4м.

Коэффициент δ₂ определяем по формуле (3.27)

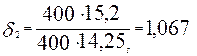
Коэффициент  δ₃ =1.

Проверку прогиба производим по формуле 3.26.

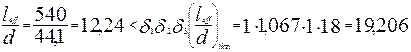
Жёсткость сечения ригеля обеспечена.