Проектирование несущих конструкций многоэтажных зданий, страница 5

Для практических расчётов рекомендуется метод предельны усилий. Для прямоугольного сечения с одиночной арматурой условия равновесия определяются из рисунка 3.3.

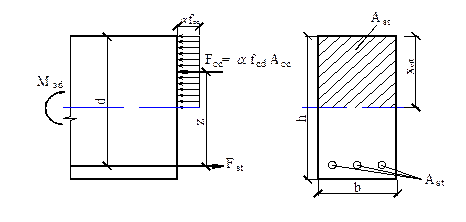
Рисунок 3.3 – Схемы распределения напряжения для прямоугольного сечения с одиночной арматурой

Для данной схемы (рисунок 3.3) можно составить три уравнения равновесия:

- уравнение моментов относительно растянутой арматуры

       (3.8)

или с учётом

     ;              (3.8.1)

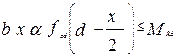
- уравнение моментов относительно линии действия сжимающей силы F_cc

    (3.9)

- уравнение суммы сил на горизонтальную ось

   (3.10)

где M_sd – расчётный изгибающий момент, вызванный действием внешней нагрузки;  M_Rd – несущая способность сечения при изгибе;

Предельное усилие в бетоне сжатой зоны определяется напряжением, равным расчётному сопротивлению бетона на сжатие f_cd, умноженному на коэффициент , учитывающий длительное действие нагрузки, неблагоприятный способ её приложения и принимаемый для тяжёлого и мелкозернистого бетонов классов прочности на сжатие не более C50/60 и для напрягающего бетона – 0,85, для более прочных бетонов – 0,8.

Предельные усилия в арматуре растянутой зоны определяются напряжениями, равными расчётному сопротивлению арматуры растяжению при высоте сжатой зоны сечения меньше граничной ().

Прочность конструкции определяется предельными усилиями в сжатом бетоне, сжатой и растянутой арматуре при высоте условной сжатой зоны меньше граничной.

Относительная высота сжатой зоны, при которой напряжения в растянутой арматуре достигают предела текучести, определяется по формуле

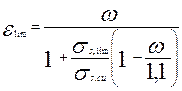 (3.11)

где  - коэффициент полноты эпюры напряжений, определяемый по эмпирической формуле

,    (3.12)

 - коэффициент, принимаемый 0,85 для тяжёлого бетона; =500Н/мм²

При одиночном армировании для подбора сечения арматуры определяется коэффициент

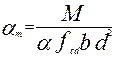    (3.13)

Затем по таблице (приложение Ж [2]) определяется коэффициент . Требуемая площадь растянутой арматуры определяется из условия (3.10)

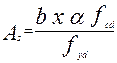  (3.14)

Подбор арматуры и расчёт несущей способности прямоугольного ригеля при наличии всех стержней и двух оборванных стержнях приведён в таблице (3.4)

Таблица 3.4 – Подбор арматуры в ригеле и расчёт его несущей способности

Исходные данные: h=500мм, b=200мм, класс  бетона C30/37, f_cd=20МПа, арматура класса S400, f_yd=365Н/мм².