3. РАСЧЁТ РИГЕЛЯ
3.1 Нагрузки
Кроме нагрузок приведённых в таблице 2.1, необходимо учесть нагрузку от собственного веса неразрезного ригеля. Сечение его достаточно точно можно определить по формулам:
|
fcd – расчётное сопротивление бетона. |
Рисунок 3.1 Поперечное сечение ригеля |
Нагрузка от собственного веса ригеля, кН/м,
g=25bh, где b и h – принятая ширина (b=10, 12, 15 и далее кратно 5см) и высота сечения (кратно 5см до 60см и 10см при большей высоте).
Расчётный изгибающий момент для свободно опёртой балки определяется по формуле:
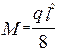 , с
учётом полных нагрузок (таблица 2.1) ,определяем расчётный изгибающий момент,
получим:
, с
учётом полных нагрузок (таблица 2.1) ,определяем расчётный изгибающий момент,
получим:
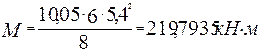
По формулам (3.1), приняв класс бетона C30/37, с учётом найденного изгибающего момента определим h0, b
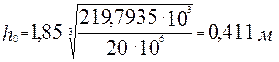 ,
,
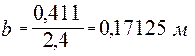
Определим полную высоту сечения h по формуле
![]() , где
, где ![]() принимают равным 50…80мм (принимаем
принимают равным 50…80мм (принимаем ![]() равным 50мм), получим
равным 50мм), получим
![]()
Принимаем b=20см; h=50см.
Определяем нагрузку от собственного веса ригеля
g=25bh=25 0,2 0,5=2,5 кН/м.
Нагрузки, действующие на ригель сводим, в таблицу 3.1
Таблица 3.1 – Нагрузки на ригель
|
Нагрузки |
Нагрузки, кПа |
||
|
Нормативные |
|
расчётные |
|
|
Постоянные |
|||
|
1 Пол |
3,0 |
1,2 |
3,6 |
|
2 Плита перекрытия |
18,0 |
1,1 |
19,8 |
|
3 Ригель (b=20см; h=50см) |
2,5 |
1,1 |
2,75 |
|
И т о г о |
23,5 |
26,15 |
|
|
Временные |
|||
|
4 Стационарное оборудование |
9,0 |
1,3 |
11,7 |
|
5 Вес людей и материалов |
21,0 |
1,2 |
25,2 |
|
И т о г о |
30,0 |
36,9 |
|
|
Суммарные |
|||
|
6 Полные |
53,5 |
63,05 |
|
|
7 В т.ч. длительные |
32,5 |
37,85 |
|
3.2 Статический расчёт
Настилы с гладким потолком передают нагрузку на ригель в виде равномерно распределённой, а ребристые настилы - через систему сосредоточенных сил. По правилам строительной механики при меньшем числе плит необходимо найти опорные моменты (лишние неизвестные), а затем пролётные.
Изгибающие моменты в пролётном и опорном сечениях определяются по формулам:
![]() (3.3), где
(3.3), где ![]() ,
, ![]() -
табличные коэффициенты, зависящие от характера загружения неразрезной балки;
-
табличные коэффициенты, зависящие от характера загружения неразрезной балки; ![]() ,
, ![]() -
соответственно величины постоянных временных распределённых нагрузок;
-
соответственно величины постоянных временных распределённых нагрузок; ![]() - пролёт ригеля (для опорного момента –
наибольший примыкающий к опоре).
- пролёт ригеля (для опорного момента –
наибольший примыкающий к опоре).
Табличные коэффициенты берутся из приложения А [2].
Расчёт с помощью таблиц разрешается для балок, пролёты которых равны или отличаются друг от друга не более чем на 10%.
В целях экономии материалов и унификации армирования производится перераспределение моментов. Оно сводится, как правило, к понижению и выравниванию опорных моментов. Понижение моментов на первой промежуточной опоре не должно превышать 30% в целях избежания чрезмерного раскрытия трещин. Пролётные моменты при рассматриваемом загружении увеличиваются, но, как правило, не превосходят значений при невыгодном загружении на пролётный момент.
В таблице 3.2 приведены значения максимальных моментов для пятипролётного ригеля при g=26,15кН/м, p=38,1кН/м, l=5.4м. Вычисление их производилось по формуле (3.3).
При первом и втором загружениях вычислены пролётные моменты, которые для загружаемых пролётов будут максимальными. Максимальные пролетные моменты можно вычислить по формуле, условие равенства пролётных и опорных моментов в свободно опёртой балке:
![]() , (3.4)
, (3.4)
где M0 – момент в свободной балке; Msup,l , Msup,r – абсолютные значения моментов на левой и правой опорах с учётом перераспределения усилий.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.