Проверку нормальных напряжений в рамах следует производить:
- в сечениях по биссектрисе и нормальных к поясу или стойке у конца биссектрисного сечения в рамах с зубчатым клеевым стыком в карнизном узле;
- в криволинейной части в месте наибольшего момента гнутоклееных рам и в нормальных сечениях ригеля и стойки в месте зубчатого стыка (в рамах с гнутоклееной вставкой);
- в сечении, нормальном к оси ригеля у конца подкоса и между стойкой и подкосом (если на этом участке применено меньшее сечение, чем у конца подкоса) для рам с угловыми и опорными подкосами. Для этих рам проверяется прочность стоек и подкосов.
В других сечениях ригеля и стойки проверки нормальных напряжений не требуется, если высота сечения ригелей в коньке hк не менее 0,3hку, а высота сечения стоек у опор hп не менее 0,4hку , где hку - высота сечения элементов в карнизном узле, назначаемая по расчету, но не менее 1/20 - 1/30 L.
Проверку на скалывание следует производить в пяте стоек и в сечениях над подкосами (если таковые имеются в раме).
При расчете
карнизного узла, выполненного на зубчатый стык по биссектрисе, должна
учитываться криволинейность эпюры напряжений (рис.3.1), для чего расчетная
высота биссектрисного сечения принимается равной [II, с.
75] ![]() , где hб
- высота биссектрисного сечения:
, где hб
- высота биссектрисного сечения:
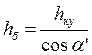 , где hку
- высота сечения элементов в карнизном узле; α' - угол между
биссектрисным сечением и горизонталью,
, где hку
- высота сечения элементов в карнизном узле; α' - угол между
биссектрисным сечением и горизонталью, ![]() ,
,
φ - половина угла между наружными гранями элементов в карнизном узле.
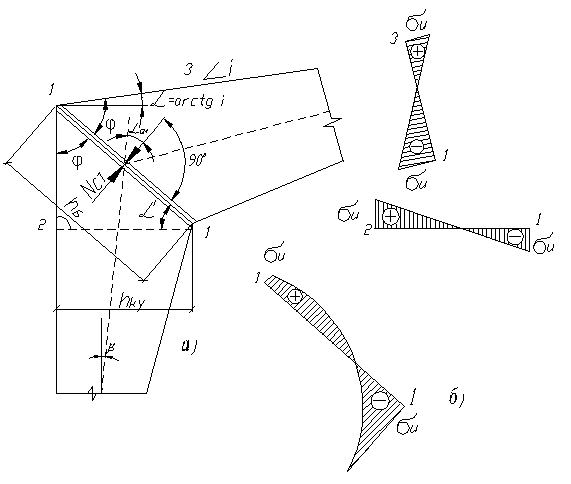
К расчету карнизного узла с зубчатым стыком по биссектрисному сечению
![]()
![]() - наибольший острый угол между нормалью к сечению и
направлением волокон сминаемого элемента.
- наибольший острый угол между нормалью к сечению и
направлением волокон сминаемого элемента.
а) - схема узла; б) - эпюры напряжений в расчетных сечениях
Рис. 3.1
Расчетная площадь и момент сопротивления биссектрисного сечения
![]() ; (3.1)
; (3.1)
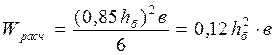 , (3.2)
, (3.2)
где hб - высота биссектрисного сечения карнизного узла; в - ширина сечения.
Проверка краевых напряжений в биссектрисном сечении производится по формуле (8.3) [II]
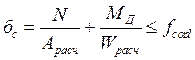 , (3.3)
, (3.3)
где МД - изгибающий момент в карнизном узле с учетом деформаций рамы,
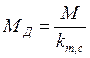 ;
;
![]() - коэффициент, учитывающий дополнительный
момент от продольной силы вследствие деформации рамы,
- коэффициент, учитывающий дополнительный
момент от продольной силы вследствие деформации рамы,
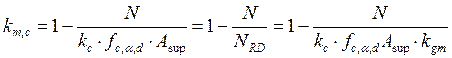 ; (3.4)
; (3.4)
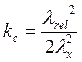 ;
;
![]() - расчетное сопротивление древесины
сжатию (смятию) под углом
- расчетное сопротивление древесины
сжатию (смятию) под углом ![]() , образуемым
биссектрисным сечением с нормалью к оси стойки,
, образуемым
биссектрисным сечением с нормалью к оси стойки,
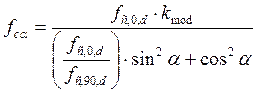 ; (3.5)
; (3.5)
fс,0,d
- расчетное сопротивление древесины соответствующей породы и сорта сжатию вдоль
волокон; fс,90,d - то же сжатию по всей
площади поперек волокон (п. 3, табл. 3 [7]; β' - угол наклона оси стойки
к вертикали (рис.3.1); ![]() - гибкость Эйлера, определяемая
по таблице формуле (7.15) СНБ 5.05.01-2000
- гибкость Эйлера, определяемая
по таблице формуле (7.15) СНБ 5.05.01-2000
Для элементов
переменного по высоте сечения площадь Asup
следует принимать для максимального по высоте сечения (см. примечание в п. 4.17
СНиП II-25-80), т. е. ![]() .
.
Коэффициент кg,m , учитывающий переменность высоты сечения, принимается по табл. 7.5 СНБ 5.05.01-2000. Для полурам, не имеющих закреплений из плоскости кромки.
![]() , где
, где 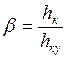 ; hк - высота сечения в коньке.
; hк - высота сечения в коньке.
Гибкость полурамы в плоскости изгиба
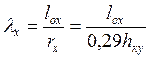 , (З.6)
, (З.6)
где l ox - расчетная длина, равная длине полурамы по осевой линии, т. е.
![]() (п. 6.28 [7]); Scт
, Sриг - соответственно длины оси
стойки и ригеля (рис.2.1, а).
(п. 6.28 [7]); Scт
, Sриг - соответственно длины оси
стойки и ригеля (рис.2.1, а).
При невыполнении условия прочности (3.3) вместо зубчатого стыка по биссектрисному сечению необходимо применить трапециевидную или пятиугольную вставку. В этом случае, поскольку угол встречи элементов α уменьшается в 2 раза, расчетное сопротивление fcαd по формуле (3.5) существенно возрастет. Если при этом условие прочности (3.3) не выполнится, необходимо применить гнутоклееную вставку или увеличить сечение элементов в карнизном узле (рис.1.1, д).
Окончательную проверку прочности полурам следует вести по формуле (7.31) как для сжато-изогнутых элементов.
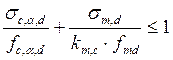 , где
, где
![]() =
=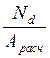 - расчётное напряжение
сжатия;
- расчётное напряжение
сжатия;
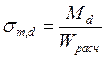
![]() - расчётное напряжение
изгиба;
- расчётное напряжение
изгиба;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.