Проектирование профиля кулачка с роликом и коромыслом. Синтез зубчатого механизма

5.  СИНТЕЗ КУЛАЧКОВЫХ МЕХАНИЗМОВ

5.1.  По заданному определяем тип и фазовые углы кулачкового механизма

Дважды проинтегрировав уравнения  с учетомначальных условий, получаем выражения для определения аналогаскорости и угла поворота коромысла:

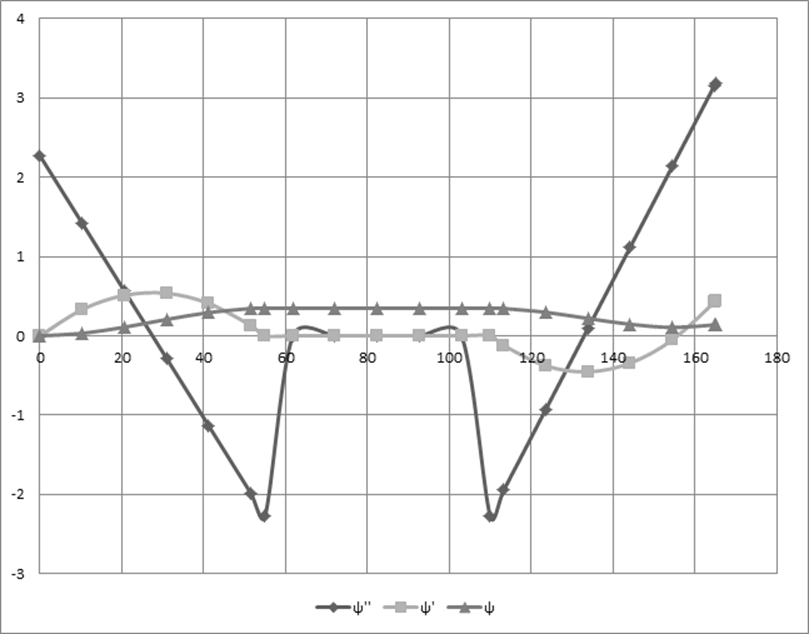
Углы поворота кулачка, соответствующие подъему и опусканию коромысла, делим на восемь равных частей. Рассчитываем и заносим в таблицу 5.1 для каждого положения.

Таблица 5.1

Для определения начального радиуса кулачка R0 не обходимо найти l0-расстояние между центрами вращения кулачка и коромысла и ψ0 - угол между нижним положением коромысла и межосевой линией О1О2. Параметры ψ0 и l0 находим из условий ограничения угла давления и получения минимальных размеров кулачкового механизма. Для случая вращения кулачка и коромысла на фазе подъема в противоположных направлениях:

где ψ- угол поворота коромысла на фазе подъема, при котороми ψ’_m= ψ’_φmax; ψп – уголповорота коромысла на фазе опускания, при котором ψ‘_ф=.ψ’_φmin

Диаграмма движения коромысла

Находим значения Ψ0 и l0:

Ψ0 =                     l0 =

Определив Ψ0 и l0 находим начальный радиус кулачка:

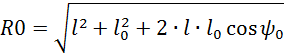
Центровой профиль кулачка рассчитываем в полярнихкоординатах по формулам:

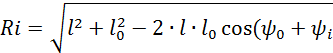
Где  - величина радиуса вектора центрового профиля кулачка; α- полярный угол; β и β₀ – углы, определяемые из выражений

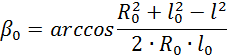
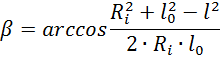
Для углов поворота кулачка значения полярных координат и углов  приведены в таблице. Для определения профиля кулачка выбираем радиус ролика из условия r ≤ 0,4Rо = 0.4*78 = 31 мм. Принимаем радиус ролика r = 25мм. Величину радиуса-вектора и полярный угол профиля кулачка рассчитываем по формулам

где

где

здесь угол  при вращении кулачка и коромысла в противоположных направлениях. В выражении Δα – угол между радиусом вектором профиля кулачка

В результаты расчета положений механизма приведены в таблице

Для построения центрового профиля и профиля кулачка выбираем масштабный коэффициент μ= 2 мм/мм. С учетом принятого масштабного коэффициента из точки О₁  - центра вращения кулачка - проводим окружность с радиусом R₀ и дугу с радиусом l₀, на которой выбираем точку O₂ - центр вращения коромысла. Из точки О₂ радиусом, равным l, делаем засечку на окружности радиуса R₀. Точка A₀ является началом фазы подъема коромысла. От начального радиуса-вектора O₁A₀ в сторону, противоположную вращению кулачка, откладываем углы аi, на сторонах которых отмечаем соответственно радиусы Ri. Центровой  профиль кулачка на участках, соответствующих верхнему и нижнему выстоям коромысла, очерчиваем по дугам окружностей с радиусами R и R. Точки А₀...А₂₀. соединяем плавной кривой. Профиль кулачка строим аналогично, откладывая на сторонах полярных углов а_пi. величины радиусов-векторов R_ni.

6  СИНТЕЗ ЗУБЧАТОГО МЕХАНИЗМА

Синтез зубчатого механизма состоит в подборе чисел зубьев колес по заданной схеме и передаточному отношению. При решении задачи используются условия соосности, сборки и соседства. Кроме того, числа зубьев колес должны находиться в приделах от 17 до 150. Для подбора чисел зубьев колес и числа сателлитов должны быть заданы схема механизмов и передаточное отношение

6.1  В соответствии с данными записываем три уравнения и три неравенства:

уравнение заданного передаточного отношения

(4,1)

уравнение соосности колес 1 и 3

                                      (4,2)

уравнение сборки

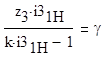(4,3)

условие соседства

                              (4,4)

6.2  Из уравнения 4,3 находим знасения z3, лежащие в пределах от 51 до 150, при которых    будет целым числом

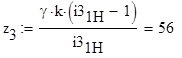
Число сателлитов к выбираем в пределах от 3 до 6

В таблице 6.1 приведены числа зубьев колеса 3 при различных значениях   и   

6.3  Из уравнений 4,1 и 4,2 выразим z2’ через z2 и z3

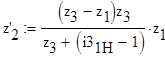
Подставляя в эту формулу найденные значения z3 и задаваясь