векторы, совпадающие с направлением обхода, учитываются со знаком «+» а не совпадающие - со знаком «-». Затем проецируем уравнение на оси координат.
Рассмотрим
первый контур ![]() :
:
![]() (3.1)
(3.1)
Уравнению (3.1) соответствуют два уравнения проекций на оси координат:
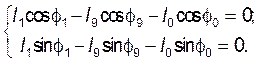 (3.2)
(3.2)
Среди
величин, входящих в уравнения (3.2), переменными являются ![]() ,
, ![]() и
и ![]() . Угол
. Угол ![]() является
обобщённой координатой механизма и может быть определен в данном положении как
является
обобщённой координатой механизма и может быть определен в данном положении как ![]() , где
, где ![]() - угол
поворота кривошипа, соответствующий крайнему правому положению механизма и началу
рабочего хода. Из уравнений (3.2) подлежат определению переменные параметры
- угол
поворота кривошипа, соответствующий крайнему правому положению механизма и началу
рабочего хода. Из уравнений (3.2) подлежат определению переменные параметры ![]() и
и ![]() . Находим
угол
. Находим
угол ![]() :
:
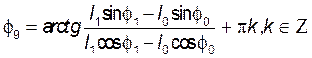 .
.
Из чертежа
видно, что ![]() - угол третьей четверти, значит, k=1.
- угол третьей четверти, значит, k=1.
Находим
модуль вектора ![]() :
:
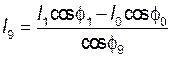 .
.
Составим
контур ![]() :
: ![]()
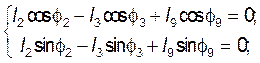 (3.3)
(3.3)
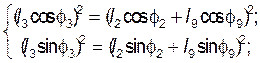
![]()
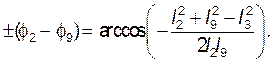 (3.4)
(3.4)
Из рисунка 3.3 видно, что ![]()
Но 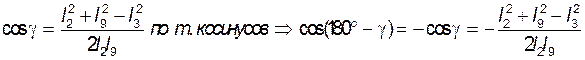 .
.
Тогда выражение (3.4) примет вид: 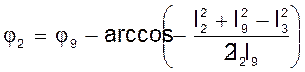 .
.
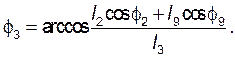
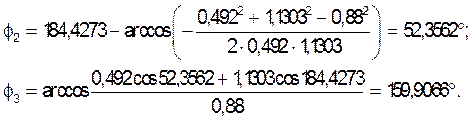
Рассмотрим контур ![]() :
: ![]()
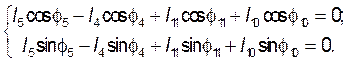 (3.5)
(3.5)
Так как ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , то решая
систему (3.5), получим
, то решая
систему (3.5), получим

Запишем координаты центра тяжести звена 5:
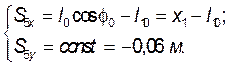 (3.6)
(3.6)
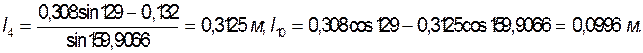
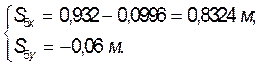
Для нахождения координат центров масс звеньев 2 и 3 составляем
условия замкнутости контуров ![]() соответственно:
соответственно:
![]() (3.7)
(3.7)
![]() (3.8)
(3.8)
Из уравнений (3.6) и (3.7), учитывая, что ![]() , находим координаты точек
, находим координаты точек ![]() :
:
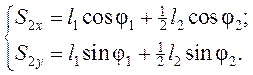 (3.9)
(3.9)
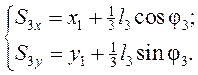 (3.10)
(3.10)
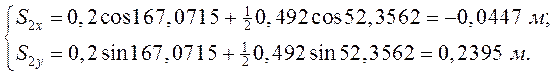
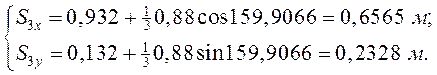
Все вычисленные величины сравниваем с соответствующими величинами, найденными из плана механизма. Результаты сравнения приведены в таблице 3.3.
Таблица 3.3. Сравнение результатов расчёта положений звеньев
графическим и аналитическим методами
|
Величина |
|
|
|
|
|
|
|
|
Графически |
167,0713 |
52,3559 |
159,9068 |
0,3125 |
184,4273 |
1,1303 |
0,0997 |
|
Аналитически |
167,0715 |
53,3562 |
159,9066 |
0,3125 |
184,4273 |
1,1303 |
0,0996 |
|
Отклонение, |
- |
- |
- |
- |
- |
- |
- |
3.4. Определение аналогов скоростей и ускорений.
3.4.1. Определение аналогов скоростей аналитическим методом.
Так как
аналоги скоростей и ускорений не зависят от закона изменения обобщенной
координаты, принимаем ![]() рад/с.
рад/с.
Аналитическое
определение аналогов скоростей основано на дифференцировании по обобщенной
координате векторного контура ![]() и
систем уравнений (3.5), (3.6), (3.9) и (3.10). Рассмотрим контур
и
систем уравнений (3.5), (3.6), (3.9) и (3.10). Рассмотрим контур ![]() :
:
![]()
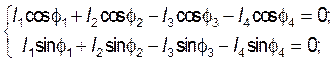
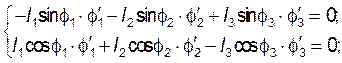 (3.11)
(3.11)
где ![]() - аналог угловой скорости звена (1), в
расчетах примем
- аналог угловой скорости звена (1), в
расчетах примем ![]() - аналог угловой скорости звена
(2);
- аналог угловой скорости звена
(2); ![]() - аналог угловой скорости звена (3).
- аналог угловой скорости звена (3).
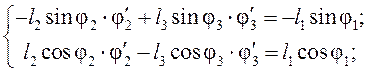
![]()
![]()
![]()
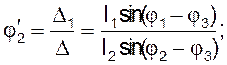
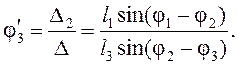
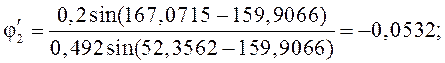
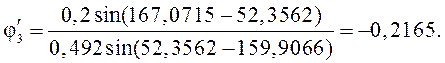
Дифференцируем
систему (3.5), учитывая ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() :
:
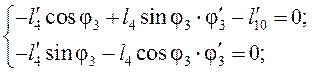 (3.12)
(3.12)
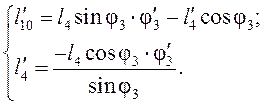
Здесь ![]() - аналог относительной скорости D
относительно E и
- аналог относительной скорости D
относительно E и ![]() - аналог абсолютной скорости
точки D.
- аналог абсолютной скорости
точки D.
Аналог скорости центра масс звена 5 получим, дифференцируя систему (3.6):
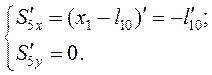 (3.13)
(3.13)
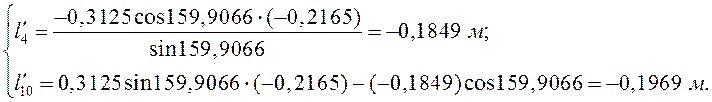
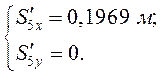
Аналоги скоростей центров масс звеньев (2) и (3) получаем в проекциях на оси координат, дифференцируя по обобщённой координате уравнения (3.9) и (3.10):
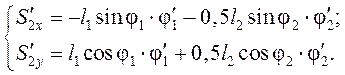 (3.14)
(3.14)
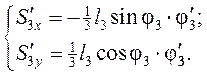 (3.15)
(3.15)
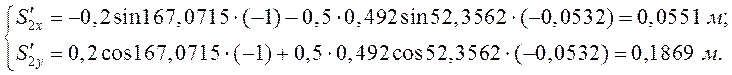
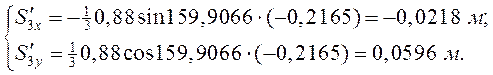
3.4.2. Определение аналогов ускорений аналитическим методом.
Аналитическое определение аналогов ускорений основано
на дифференцировании по обобщённой координате уравнений (3.11) - (3.15). Найдем
аналоги угловых ускорений ![]() и
и ![]() звеньев 2 и 3:
звеньев 2 и 3:
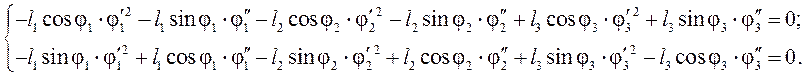 Так как
Так как ![]() и
и ![]() , то
перенеся слагаемые, не содержащие
, то
перенеся слагаемые, не содержащие ![]() и
и ![]() в правую часть, получим:
в правую часть, получим:
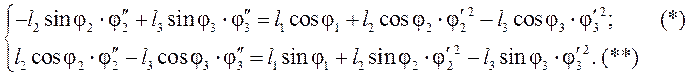
Обозначим правые части полученных уравнений (*) и
(**) через ![]() и
и ![]() . Тогда
. Тогда
![]()
![]()
![]()
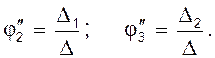
![]()
![]()
![]()
![]()
![]()

Для
вычисления ![]() дифференцируем уравнения (3.12):
дифференцируем уравнения (3.12):
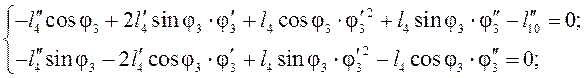
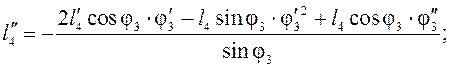
![]()
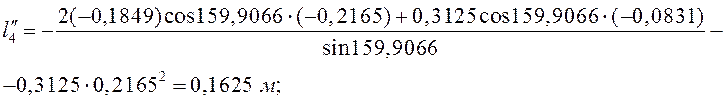
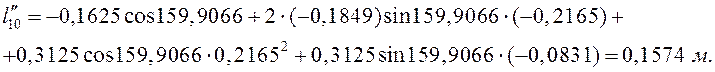
![]() - аналоги относительного и абсолютного ускорения
точки D соответственно.
- аналоги относительного и абсолютного ускорения
точки D соответственно.
Дифференцируя по обобщённой координате уравнения (3.13)-(3.15), находим аналоги ускорений центров масс звеньев 5, 2 и 3 в проекциях на оси координат:
![]()
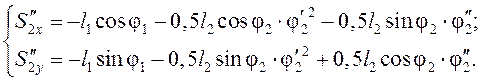
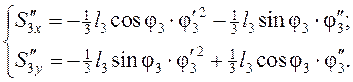
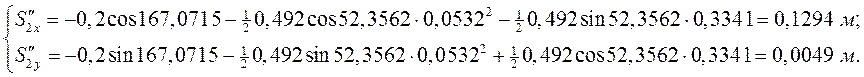
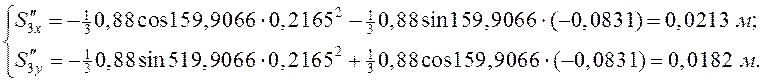
3.4.3. Определение аналогов скоростей графическим методом.
Определение аналогов скоростей
графическим методом основано на построении плана скоростей для четвертого
положения механизма при ![]() . Так как аналоги
скоростей и ускорений не зависят от закона изменения обобщенной координаты,
принимаем
. Так как аналоги
скоростей и ускорений не зависят от закона изменения обобщенной координаты,
принимаем ![]() .
.
План скоростей механизма строим в следующем порядке:
1) находим скорость точки А относительно точки ![]() :
:
![]()
2) из полюса плана скоростей p откладываем отрезок pa= 50 мм, изображающий вектор скорости точки A.
3) подсчитываем масштабный коэффициент скоростей: 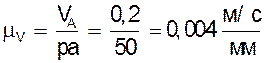 ;
;
4) скорость точки В определяем из следующего уравнения, решая его графически:
![]() .
.
Через точку a проводим перпендикуляр к звену 2 - направление скорости ![]() , а через полюс p – перпендикуляр к звену 3
- направление скорости
, а через полюс p – перпендикуляр к звену 3
- направление скорости ![]() , до пересечения этих прямых в точке b. Векторы
, до пересечения этих прямых в точке b. Векторы ![]() и
и ![]() изображают скорости
изображают скорости ![]() и
и ![]() . Величина скорости
. Величина скорости ![]() .
.
5) найдем угловую скорость звена (2): 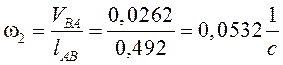 ,
,
величина скорости: ![]() , а
угловая скорость звена (3):
, а
угловая скорость звена (3): 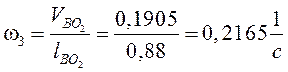 .
.
5) определим скорость точки Е:
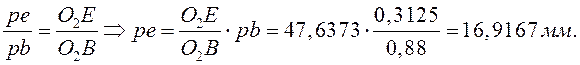
![]() .
.
6) скорость точки D определим из уравнения:
![]() .
.
Через точку e проводим прямую, параллельную ![]() -
направление скорости
-
направление скорости ![]() , а через точку p – горизонтальную
прямую - направление скорости
, а через точку p – горизонтальную
прямую - направление скорости ![]() . Полученные векторы
. Полученные векторы ![]() и
и ![]() изображают относительную и абсолютную скорости точки D, а
также точек C и
изображают относительную и абсолютную скорости точки D, а
также точек C и ![]() . Величины этих скоростей имеют вид:
. Величины этих скоростей имеют вид:
![]() ,
, ![]()
7) находим положения точек ![]() на плане скоростей:
на плане скоростей:
![]() .
.
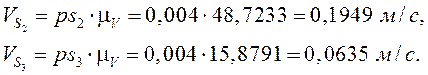
Таблица 3.4. Сравнение результатов расчёта аналогов скоростей звеньев графическим и аналитическим методами
|
Величина |
|
|
|
|
|
|
|
|
|
|
Графически |
0,0533 |
0,2165 |
0,185 |
0,197 |
0,0551 |
0,1869 |
0,0218 |
0,0597 |
0,197 |
|
Аналитически |
-0,0532 |
-0,2165 |
-0,1849 |
-0,1969 |
0,0551 |
0,1869 |
0,0218 |
0,0596 |
0,1969 |
|
∆% |
- |
- |
- |
- |
- |
- |
- |
- |
- |
3.4.4. Определение аналогов ускорений графическим методом.
Задачу решаем путем построения плана
ускорений, считая ![]() постоянной величиной.
постоянной величиной.
1) находим ускорение точки А. Так
как ![]() , то
, то ![]() . Полное
ускорение точки А равно нормальной составляющей
. Полное
ускорение точки А равно нормальной составляющей ![]() ,
которая направлена по звену
,
которая направлена по звену ![]() к центру
к центру ![]() .
.
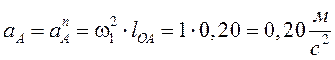
2) из точки π- полюса плана ускорений- откладываем
вектор, изображающий ускорение точки А в виде отрезка ![]() .
.
3) Подсчитываем масштабный коэффициент ускорений:
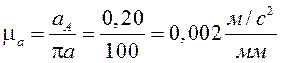
4) ускорение точки В, являющейся общей для звеньев (2) и (3), находим решая графически следующую систему уравнений:
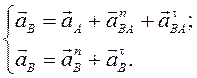
Определим ![]() и
и ![]() :
:
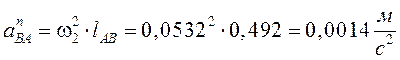 - направлено
параллельно АВ от В к А;
- направлено
параллельно АВ от В к А;
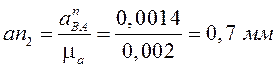 ;
;
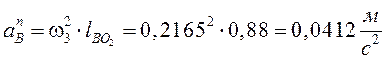 - направленно
параллельно
- направленно
параллельно ![]() от В к
от В к ![]() ;
;
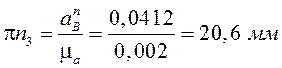 .
.
Векторы ![]() и
и ![]() направлены перпендикулярно звеньям 2 и 3 соответственно.
направлены перпендикулярно звеньям 2 и 3 соответственно.
Через точки ![]() и
и
![]() плана ускорений проводим направления
векторов касательных ускорений, пересечение которых дает точку b,
плана ускорений проводим направления
векторов касательных ускорений, пересечение которых дает точку b, ![]() - графическое изображение ускорения точки
В. Далее находим:
- графическое изображение ускорения точки
В. Далее находим:
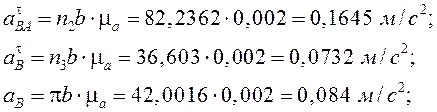
Угловые ускорения звеньев 2 и 3:
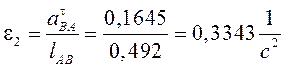 ;
; 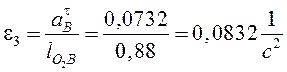 .
.
5) Определим ускорение точки Е, воспользовавшись теоремой подобия:
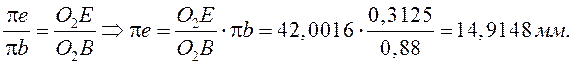
6) Ускорение точки D найдем, решая
уравнение ![]()
Кориолисово ускорение равно:
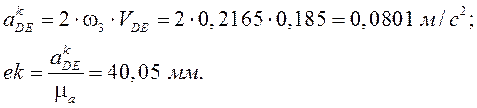
Направление его определяется как векторное
произведение векторов ![]() .
.
Через точку k плана ускорений проводим прямую, параллельную
![]() -
направление переносного ускорения
-
направление переносного ускорения ![]() , через полюс
, через полюс ![]() - горизонтальную
- горизонтальную
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.