Кинематический анализ механизма вязального аппарата

аргументов всех тригонометрических функций вычитаем угол φ₅:

откуда

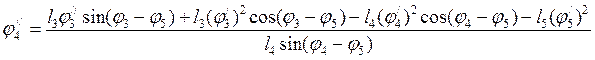          (3.31)

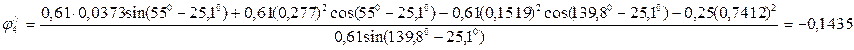
Из второго уравнения находим

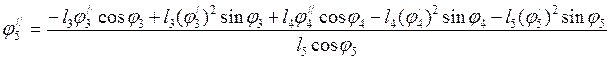          (3.32)

Дифференцируя по обобщенной координате уравнения (3.25) и (3.26), устанавливаем аналоги ускорений центров масс звеньев 3 и 4 в проекциях на оси координат:

                        (3.33)

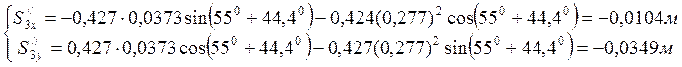
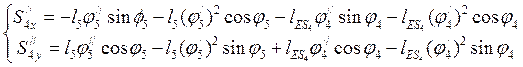              (3.34)

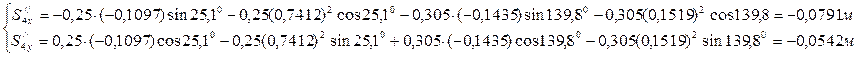
Результаты расчетов аналогов скоростей и ускорений для третьего положения приведены в табл. 3.3, 3.4.

3.4. Построение планов скоростей и ускорений

3.4.1. Определение аналогов скоростей исследуемого механизма графическим методом

Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем ω₁ = 1 рад/сек.

План скоростей механизма строим в следующем порядке:

1) находим скорость точки В:

;

2) из полюса плана скоростей р откладываем отрезок рв₁ = 80 мм, изображающий вектор скорости точки В звена 1;

3) подсчитываем масштабный коэффициент скоростей:

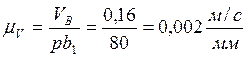
4) скорость точки В, принадлежащей звену 3, находим, раскладывая движение на переносное (вращательное) вместе с точкой В, принадлежащей звену 1 и относительное (поступательное) по отношению к точке В₁. В абсолютном движении точка В₃ вращается вокруг точки С. Поэтому:

.

Через точку в₁ проводим линию, параллельную ВС, а через полюс р – линию, перпендикулярную ВС, до пересечения их в точке в₃. Вектор  изображает скорость точки В₃;

5) скорость точки D звена 3 определяем, используя теорему подобия

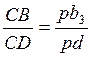, откуда

.

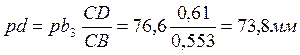Вектор скорости точки D повернут на 55⁰ относительно вектора скорости точки В₃

6) для определения скорости точки Е раскладываем плоскопараллельное движение звена 4 на переносное (поступательное) вместе с точкой D и относительное (вращательное) вокруг точки D. С другой стороны, точка Е находится в абсолютном движении вокруг неподвижной точки К. Поэтому:

.

Через точку d проводим линию, перпендикулярную DE, а через полюс р – линию, перпендикулярную ЕК , до пересечения их в точке е. Вектор  изображает скорость точки Е;

7) положения точек s₃и s₄ на плане скоростей находим, воспользовавшись теоремой подобия:

,

.

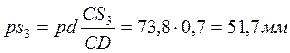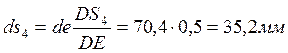Векторы  и  изображают скорости и ;

8) из плана скоростей находим:

,

,

,

.

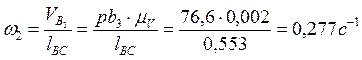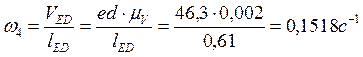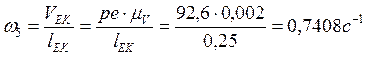Определяем аналоги линейных и угловых скоростей:

,         ,

,         .

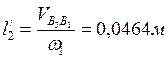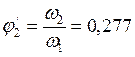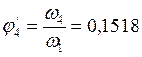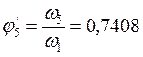В табл. 3.3 приведены значения аналогов скоростей для расчетного положения, полученные аналитическим и графическим методами.

Таблица 3.3

Результаты расчета аналогов скоростей

3.4.2. Определение аналогов ускорений исследуемого механизма графическим методом

Задачу решаем путем построения плана ускорений, считая ω₁ постоянной величиной.

1) находим ускорение точки В₁. Полное ускорение точки В₁ равно нормальной составляющей , которая направлена по линии AB к центру A

;

2) из точки р – полюса плана ускорений откладываем вектор, изображающий ускорение точки B, в виде отрезка рb₁ = 160 мм;

3) подсчитываем масштабный коэффициент ускорений:

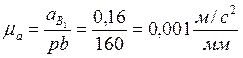
4) Ускорение точки B₃, звена 3, находим из уравнения:

,                                             (3.35)

в котором  – относительное ускорение,  – кориолисово ускорение:

.

Направление кориолисова ускорения определяется поворотом относительной скорости  на 90⁰ по направлению переносной угловой скорости .

Ускорение  в свою очередь раскладывается на нормальную и касательную составляющие:

.

Нормальное ускорение вычисляем по формуле:

,

Отрезок, изображающий в миллиметрах вектор этого ускорения, равен:

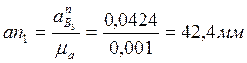
Уравнение (3.35) решаем графически. Через точку b₁ проводим линию, перпендикулярную АВ, и откладываем на ней отрезок b₁k, изображающий кориолисово ускорение:

.

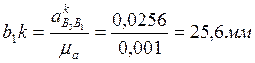Через полюс р проводим линию, вдоль которой направлено нормальное ускорение точки B₃. Через точку k проводим линию, параллельную ВC, вдоль которой направлено относительное ускорение, а через точку п₁ – направление вектора касательного ускорения, пересечение которых определяет точку b₃ – конец вектора искомого ускорения точки B₃.

5) для расчета ускорения точки D звена 3 используем теорему подобия:

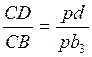, откуда

.

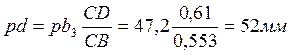Вектор ускорения точки D повернут на 55⁰ относительно вектора ускорения точки В₃

6) для определения ускорения точки E записываем два векторных уравнения, рассматривая движение этой точки вначале с четвертым звеном