Контрольные параметры рассчитаны с помощью программы ТММ21 по формулам (3.21) – (3.24) и занесены в таблицу 3.5.
Расчетное число зубьев в длине общей нормали для прямозубых колес zw, [1]:
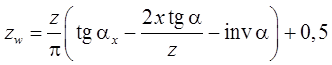 , (3.21)
, (3.21)
где aх — угол профиля в точке на концентрической окружности диаметра dx.
Длина общей нормали W, мм [1]:
W = (p (zw – 0,5) + 2x tga – z inva) mcosa. (3.22)
Длина постоянной хорды ![]() , мм [1]:
, мм [1]:
![]() =
m (0,5p cos2a + x sin2a). (3.23)
=
m (0,5p cos2a + x sin2a). (3.23)
Высота до постоянной хорды ![]() , мм [1]
, мм [1]
![]() =
0,5(da – d –
=
0,5(da – d – ![]() tga). (3.24)
tga). (3.24)
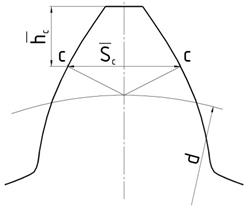
Рисунок 3.3 – Контрольные
параметры ![]() ,
, ![]()
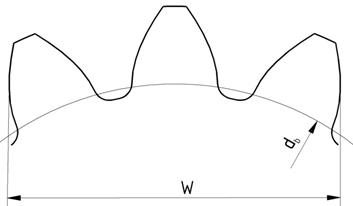
Рисунок 3.4 – Контрольный параметр W
Таблица 3.5 – Контрольные параметры
|
Параметры шестерни, m = 6 мм; z1 = 15 |
|
|
Число зубьев общей нормали |
3 |
|
Длина общий нормали, мм |
47,178 |
|
Длина постоянной хорды, мм |
9,598 |
|
Высота до постоянной хорды, мм |
5,78 |
|
Параметры колеса, z2 = 23 |
|
|
Число зубьев общей нормали |
4 |
|
Длина общий нормали, мм |
65,25 |
|
Длина постоянной хорды, мм |
9,315 |
|
Высота до постоянной хорды, мм |
5,453 |
4 СИНТЕЗ ПЛАНЕТАРНОГО МЕХАНИЗМА
4.1 Подбор числа зубьев
Числа зубьев и оптимальные по габаритам размеры получены из компьютерных расчётов, сделанных в программе ТММ12-7, таблица 4.1.
Таблица 4.1 – Основные параметры планетарного механизма
|
Редуктор Джеймса |
||
|
Число зубьев солнечного колеса |
17 |
|
|
Число зубьев сателлитов |
28 |
|
|
Число зубьев корончатого колеса |
73 |
|
|
Передаточное отношение |
5,29 |
|
|
Отклонение передаточного отношения |
- 0,0357 |
|
|
КПД редуктора |
0,94 |
|
4.2 Алгоритм компьютерного расчёта
а) Условие соосности:
z1 + z2 = z3 - z2 = δ, (4.1)
где δ – аналог делительного межосевого расстояния.
Числа зубьев
z1 = δ - z2; (4.2)
z3 = δ + z2; (4.3)
б) Величина δ:
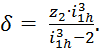 (4.4)
(4.4)
в) Предельно допускаемые передаточные отношения:
![]() (4.5)
(4.5)
где
![]() - отклонение передаточного отношения.
- отклонение передаточного отношения.
После подстановки выражений (4.5) в формулу (4.4) получены значения δmin и δmax.
г) В компьютерных расчётах внутренний цикл образуется изменением величины δ, которая задана целыми числами в интервале δmin…δmax. По формулам (4.2) и (4.3) рассчитаны числа зубьев z1 и z3. Изменение чисел зубьев z2 составляет внешний цикл.
д) Ограничение по числам зубьев осуществлено вводом zmin = 17, zmax = 150. Компьютер рассчитывает числа зубьев z1 и z3 и проверяет условия z1 ³ zmin и
z3 £ zmax. В дальнейшем величина z2 увеличивается на единицу. Пределом является z2 = zmax.
е) Проверены условия:
соосности
![]() (4.6)
(4.6)
17 + 28 = 73 – 28;
кинематическое
![]() . (4.7)
. (4.7)
соседства
![]() (4.8)
(4.8)
где nc – число сателлитов (nc = 3).
![]() 11,
11,
11 > 2.
сборки
![]() (4.9)
(4.9)
где γ – целое число, условие выполняется.
ж) Оптимизация по габаритам редуктора. Основной критерий оптимизации - минимальные габариты редуктора, связанные с числом зубьев корончатого колеса z3. В каждом цикле расчета записываются в памяти ЭВМ числа зубьев z3 и заменяются только при выполнении условия
(z3)n < (z3)n-1.
После перебора чисел зубьев z2 в интервале zmin и zmax и выполнения всех условий числа
зубьев z1, z2 и z3 выводятся на печать. з) Для оптимального варианта рассчитан механическийКПД ![]() :
:
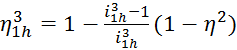 (4.10)
(4.10)
Радиусы колёс и шестерён определены по формуле:
![]() ;
(4.11)
;
(4.11)
Радиус солнечного колеса рассчитан по формуле (4.11) при m = 3 мм и z = 17 получено r = 22.5 мм.
Радиус корончатого колеса рассчитан по формуле (4.11) при m = 3 мм и
z = 73 получено r = 109,5 мм.
Радиус сателлитов рассчитан по формуле (4.11) при m = 3 мм и z = 28 получено r = 42 мм.
Радиус шестерни рассчитан по формуле (4.11) при m = 6 мм и z = 15 получено r = 45 мм.
Радиус колеса рассчитан по формуле (4.11) при m = 6 мм и z = 23 получено
r = 69 мм.
Сложный зубчатый механизм построен в масштабе μl = 0,25 мм/мм.
Общее передаточное отношение:
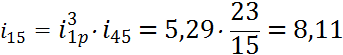
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.