Синтез эвольвентного зацепления. Синтез планетарного механизма, страница 3

ж) По компьютерной распечатке построен полный эвольвентный профиль. Для этого от полюса зацепления W отложена по дуге начальная толщина зуба s_w и разделена пополам. Точка деления соединена с центром вращения, получена ось симметрии зуба. От оси симметрии отложены половины толщин зуба по окружностям вершин s_a, промежуточной s_y, делительной s и основной s_b, получены точки профиля зуба, которые соединены плавной кривой. Построены 3 зуба на шестерне и колесе. Эвольвенты окружности впадин сопряжены кривой радиуса p_f.

з) На линии зацепления В₁В₂ отмечены точки пересечения А₁ и А₂ с окружностями вершин. А₁ А₂ — активная линия зацепления длиной .

и) Вычерчены профили зубьев штриховыми линиями в момент их входа в зацепление и выхода из зацепления (в точках А₁ и А₂).

к) На одном зубе вычерчена постоянная хорда и высота зуба до постоянной хорды .

л) На шестерне показана длина общей нормали W.

м) На чертеже обозначены буквами характерные точки. Все геометрические параметры показаны буквенными обозначениями.

н) Приведена таблица с основными параметрами: m, z₁, z₂, x₁, x₂, y, Δy, , , , a, a_w, ε_α, _. Второе значение коэффициента перекрытия найдено графическим путем по формуле:

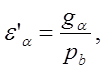                                                                                           (3.17)

где g_a – расстояние между точка А₁А₂, разделённое на масштаб.

3.3 Построение диаграммы удельного скольжения

Данные для построения диаграммы удельного скольжения рассчитаны с помощью программы ТМ21 (таблица 3.4):

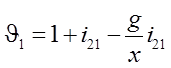;                                                (3.18)

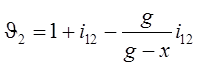          ,                                         (3.19)

где i₂₁ - передаточное отношение; g — длина линии зацепления В₁В₂, мм; х -расстояние, отсчитываемое от точки В₁, мм;

Диаграмма удельного скольжения построена в масштабе , мм [1]:

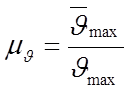,                                                   (3.20)

где - ордината диаграммы, мм, - относительное скольжение.

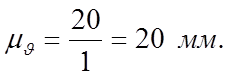
Абсциссы диаграммы ограничены активной линией зацепления А₁А₂. За ее пределами диаграммы показаны штриховыми линиями. Пространство между линиями  и  характеризует суммарное скольжение профилей друг относительно друга. Положительная часть диаграмм соответствуют скольжению на головках, отрицательная - на ножках зубьев.  

Таблица 3.4 – Относительные скольжения колеса и шестерни, удельное давление

3.4  Построение диаграммы удельного давления

Данные для построения диаграммы удельного давления γ рассчитаны по формуле (3.21) с помощью программы ТМ21 (таблица 3.4):

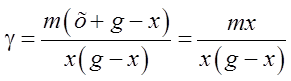                                   (3.21)

Диаграмма удельного давления строится в масштабе μ_ϒ, мм [1]:

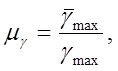                                                  (3.22)

где - максимальная ордината диаграммы, - максимальное удельное давление.

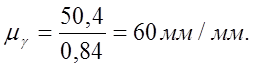
Реальные очертания диаграмма имеет в пределах активной линии зацепления А₂А₁, в зонах двухпарного зацепления, определяемых размером основного шага p_b, откладываемого от точек А₂ и А₁ в пределах активной линии зацепления, ординаты разделены пополам.

3.5  Блокирующий контур

Выбран блокирующий контур с ближайшими меньшими значениями z₁ и z₂ (z₁ = 15, z₂ = 23).

Точки, расположенные правее линии А–А, определяют коэффициенты смещения, при которых e_a < 1.

Линии В–В, С–С, D–D, Е–Е определяют коэффициенты, при которых будет происходить заклинивание зубьев: линии В–В и С–С — линии интерференции колеса, линии D–D и Е–Е — шестерни.

Линия F–F определяет неподрезание зубьев шестерни, линия G–G — колеса. Линии L–L и N–N определяют границы заострения зубьев s_a1 = 0 и s_a2 = 0.

Кривая А`-A` соответствует e_a = 1,311.

Каждая из линий x_{1 min} и x_{2 min} делит контур на 2 части: левее линии x_1min будут подрезаны зубья шестерни, а ниже линии x_2min — колеса.

3.6  Контрольные параметры