Метод графического интегрирования заключается в том, что диаграмму Мп = Мп(j) заменяют ступенчатой таким образом, чтобы на каждом участке (0-1, 1-2 и т.д.) криволинейная трапеция (криволинейный треугольник) заменялась равновеликим прямоугольником, образованным осью абсцисс, двумя вертикальными линиями границ участков и горизонтальной линией (четвертой стороной), проведенной параллельно оси абсцисс так, чтобы площадь отброшенной фигуры О равнялась площади добавленной фигуры Д .
На рис. 7.3 проиллюстрирован метод графического интегрирования. Ординаты равновеликих прямоугольников Мп.0-1, Мп.1-2 и т.д. приблизительно соответствуют средним значениям моментов, угловой шаг Δφ.
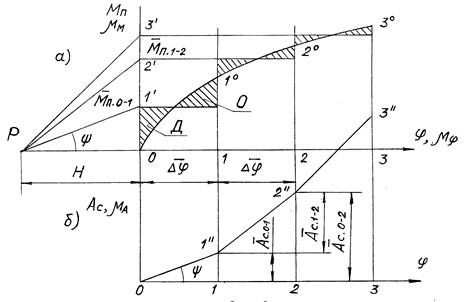
Рис. 7.3
Выбирают полюс интегрирования Р на отрезке интегрирования Н.
При выполнении курсового проекта рекомендуется принимать Н1 =
40…60 мм. Полюс интегрирования соединяют прямой (лучом) с точкой пересечения
четвертой стороны равновеликого прямоугольника с осью ординат. На первом
участке диаграммы работ из начала координат проводят отрезок, параллельный
первому лучу. Доказывается, что ордината 1–1″ на рис. 7.3, б
является графическим изображением работы сил сопротивления 
на участке 0 –1. Масштаб диаграммы работ в мм/Дж:
μА = μм μφ / Н. (7.9)
На втором участке из конца первого отрезка проводят отрезок, параллельный второму лучу. Ордината 2–2″ изображает работу сил сопротивления на участке 0 - 2 и т.д. На последнем из 12 участков ордината не будет равна нулю. Полученная ломаная линия приближенно представляет собой диаграмму Ас = Ас(j) (рис. 7.3, б). Расстояние в направлении оси ординат между соседними узловыми точками диаграммы изображает приращение работы на участке, а расстояние между начальной и текущей точками — работу за временной отрезок, равный нескольким участкам. Для механизма ДВС пример графического интегрирования диаграммы моментов приведен на рис 7.2.
Величину работы за цикл определяют величиной ординаты в мм, соответствующей концу последнего участка, делённой на масштаб mА.
7.5. Диаграммы работ и энергий
В соответствии с уравнением (7.3) в установившемся режиме за цикл (за полный оборот кривошипа) работа движущих сил равна работе сил сопротивления, т.е. в начале первого и в конце последнего участка АД = AC.
При условии постоянства момента сил сопротивления МС диаграмму работ сил сопротивления АД (для двигателей) строят соединением первой и последней точек кривой АД = AД(j) прямой линией (рис. 7.2). График МС = МС(φ) строят методом графического дифференцирования (см. раздел 4). Для этого из полюса Р проводят луч, параллельный прямой АС = АС(j) до пересечения с осью ординат. Штриховая прямая на рис. 7.2, параллельная оси абсцисс, и является графиком МС = МС(φ).
Приращение кинетической энергии за цикл DT = 0 — в соответствии с формулой (7.3). Однако в любой другой момент времени выполняется равенство (7.1): приращение кинетической энергии
.
(7.10)
График избыточных работ Аизб (приращение кинетической энергии ΔТ) строят вычитанием АС из АД (отрезки вдоль оси ординат между диаграммами АД = АД(φ) и АС = АС(φ)).
Приведенный момент инерции определяют из условия равенства кинетической энергии звена приведения сумме кинетических энергий всех звеньев механизма. Для кривошипно-ползунного механизма (см. рис. 4.1) приведенный момент инерции Iп определяется из формулы:
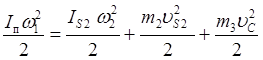, (7.11)
Для механизма ДВС вследствие равенства кинематических параметров и масс обеих диад формула (7.11) примет вид:
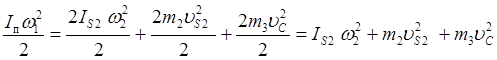. (7.12)
Следует помнить, что полный момент инерции механизма 
складывается
из момента инерции маховика 
и приведенного момента
инерции 
всех звеньев, кроме начального. Величина — переменная; величина —
постоянная, она включает в себя собственно момент инерции звена 1 (кривошипа
и других связанных с ним элементов, например, зубчатого колеса) и момент инерции
маховика, значительно превышающий другие слагаемые. Диаграмму 
строят в масштабе 
,
мм/(кг∙м2):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.