Теорема Флокэ-Ляпунова

степень исходной матрицы в этом же базисе так же будет диагональной.

При этом если:

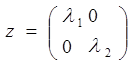,то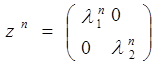

Это свойство справедливо для матриц с любым набором собственных чисел, не обязательно  симметричной.

2)Функция  матрицы  f(z) была определена, как степенной матричный ряд. Для каждого его слагаемого справедливы предыдущие рассуждения о собственных векторах и числах. Можно показать

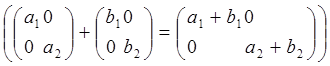,что если две матрицы A и B в каком-то базисе имеют диагональный вид, то их сумма в том же базисе так же имеет диагональный вид. Отсюда следует, что если над диагональной матрицей z проводится аналитическая операция f (раскладываемая в степенной ряд), то это не изменит диагональности результата, т.е.

.

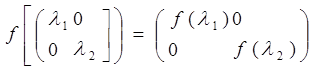Пусть теперь -собственный вектор матрицы монодромии, соответствующий мультипликатору , т.е. удовлетворяющий равенству:

Рассмотрим решение уравнения 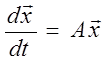 с начальным условием

Согласно изложенной ранее теории: , тогда

При «возрастании» времени на величину T решение «возрастает» в раз.

Теорема Флокэ-Ляпунова.

Свойства собственных чисел функций  матриц.

Пусть Y=f(X)-матричная функция матричного аргумента.

-собственные числа и собственные векторы матрицы X, тогда -остаются собственными для Y, а собственные числа матрицы Y

Докажем, что это так: согласно определению функции матричного аргумента f(x)-степенной ряд.

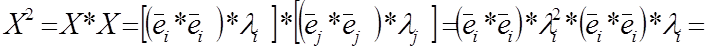
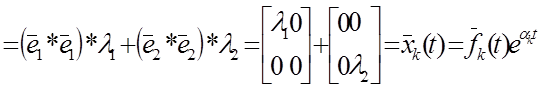
Функции  - совокупность линейно- независимых решений исходного векторного уравнения, любое решение является их линейной комбинацией. Допустим теперь эти функции описывают возмущение какого-то процесса. Он будет устойчив, если возмущения будут гаснуть. Т.к. fk(t)-ограниченная по модулю, то устойчивость, т.е. угасание возмущений будет обеспечено, если действительная часть  будет отрицательной.