Поиск решения матричного уравнения. Пример решения задачи Коши

Страница 27.

тождество. Умножим обе части на  

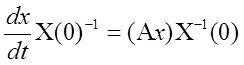
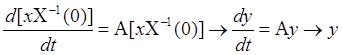решение.

Матрица y, определена таким способом низ. матрицант уравнения (3):

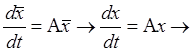
- матрицант

Поиск решения матричного уравнения.

В общем случае, когда A = A(t) – перемен. матр. решения матричного уравнения ищатся в виде ряда по степеням А, методом последовательных приближений. Суть в следующем:

диф. уравнение

dx/dt = Ax   заменяется на интегральное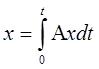 

Принимается нулевое приближение х = х₀ = I – единичная матрица, тогда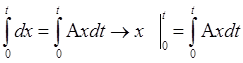 

x(t)-x(0) =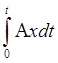

x(t) = x(0) +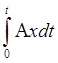

Если в качестве x(t) ищется матрицант, то удобнее всего принять, что х₀ = I – единичная матрица.

При этом х₀ = I .

Тогда итерационная формула получается вида:

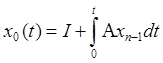
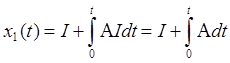
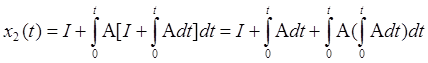
Продолжая процесс до бесконечности получаем матричный ряд. Доказано, что если А – ограниченно по норме для всех значений t, то ряд сходится.

Допустим А = const, тогда

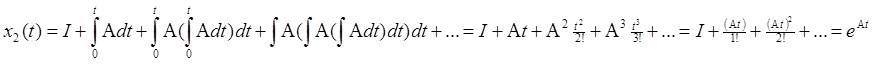
Пример. Решить задачу Коши.

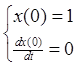
Способ 1.

x(o) = c₁+c₂=1

c₁ = 2, c₂ = -1

.

Способ  2.(матричный)

Дифиринцируем уравнение и начальные условия приводим к матричной форме.

Обозначим

x = x₁, dx/dt = x₂  

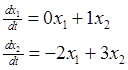
x₁(0)=1

x₂(0)=0

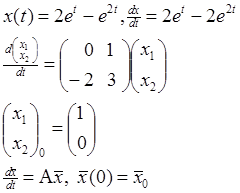
Сумма имеет постоянные коэффициенты, поэтому для матрицанта Х(t) решение имеет вид