Собственные векторы и собственные числа линейных операторов

Страница 10.

y=B*u

Собственные векторы и собственные числа линейных операторов.

Оператор А преобразует вектор х в вектор у по правилу: у=А*х.

При этом у по оношению к х меняется модульи ориентация.

Среди всех х в ряде задач представляет интерес такие, которые не меняют своей ориентации, тогда у=   х  , Ах=  *х=   Ех

Е - единичный оператор.

Отсюда получаем уравнение для поиска х

(А-  Е)х=0 (*)

Относительно х – это однородное уравнение

В*х=0, где В=А-  *Е

Т. к. размерность пространства, где определён dim х и А совпадают, то число скалярных уравнений и число неизвестных координат х равны. В этом случае уравнение имеет ненулевое решение ( т. кронекера-капелли), если ранг этого В

Rg(B)<n=dim  (равно размерности)

Т. к. В имеет квадратную матрицу датешь этого можно за счёт выполнения равенства:

DetB(   )=0.

Так как     пока не определена последнее можно считать уравнением для его определения.

Корни этого уравнения называются собственными числами или главными значениями оператора А. В приложениях    это собственная частота колебаний.

Из построенного видно, что уравнение для      алгебраическое n-порядка, значит, имеет n  корней. В зависимости от вида А корни могут быть действительные, различные, комплексные, повторяющиеся. Если             ,то корни действительные и различные. Если А связан с потенциальной энергией какого-то поля, то           .

К уравнению (*) можно прийти из других соображений.

Квадратичная форма

F=x*A*x   (          )

х – указывает какое-то направление а пространстве, для этой цели обычно используют единичные векторы.

|x|=1 или х*х=х*Е*х=1.

Тогда F=F(x) и определить те направления на которых F может достичь экстремальных значений. Возникает задача на условный экстремум. Стационарные точки определяются с помощью множителей Лагранжа согласно которому определяются стационарные точки функции

          (х)=F(x)-   (x*E*x)

d   /dx=dF/dx-2*   *Е*х=0

2(А*х-  *Е*х)

Собственным направлениям оператора А являются те, на которых он достигает стационарного значения.

Допустим задача о поиске собственных чисел и собственных векторов решена, использовать это решение можно следующим образом:

Координатная запись формы F в произвольном базисе ej имеет вид:

F=xiAijxj=x1*A11*x1+x1*A12*x2+x2*A21*x1+x2*A22*x2=A11* *x1^2+2A12*x1*x2+A22*x2^2

Если от базиса ej перейти к базису собственных векторов, выбрав их единичными, квадратичную форму можно преобразовать к каноническому виду.

F=   1y1^2+  2y2^2

При этом A=Aij*ei*ej=   1a1 a1+     2a2 a2

Т.е. в базисе ej

Ak*A= |    1  0 |

| 0     2 |

Переход от одного ортогонального базиса к другому осуществляется с помощью оператора Q

ej=Qjk*ak

Свойства:

=Е – основное ортогонального оператора (матрицы)

Рассмотрим решение задачи более подробно.

Пусть А, х принадлежит R^2, тогда

(А-  Е)*х=0  имеет следующий вид:

(А11-     А12 )*(Х1)=0

(А21    А22-  )  (Х2)

 

(А11-   )*Х1+А12*Х2=0     Система для поиска собственных

 A21*X1+(A22-   )*X2=0      векторов

Уравнение для вычисления    условие существования ненулевых решений предыдущей системы.

| А11-     A12 |=0

| A21   A22-   |

Данное уравнение записанное для определения координат системы в связи с чем возникает убеждение, что его решению собственные числа в разных системах будут разные. Доказано, что это не так, то есть собственные числа и собственные векторы не зависят от выбора системы. Отсюда следует, что коэффициенты уравнения для    должны быть инвариантными. Это действительно так. Отсюда следует, что для каждого линейного оператора инвариантом является следующее выражение:

|a11 .    .     .    |

| .                     | =A

| .                    |       

| .               a44|

l^4-J1*l^3+J2*l^2-J3*l+J4=0 – характеристическое уравнение оператора.

J1=a11+a22+a33+a44;

J2=|a11 a12|+|a22 a23|+|a33 a34|                                        

|a21 a22|  |a32 a33|  |a43 a44|

 

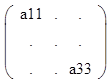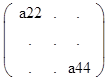J3=                   +                    + 2 определителя

J4=det(A)

Т.к. Jk одни и те же в любой системе, то они сохраняют своё значение и в системе собственных векторов, где

  

А=                

Выражая Jk по тем же формулам через элементы матрицы получим известные формулы Виеты:

J1=l1+l2+l3+l4

J2=l1*l2+l2*l3+l3*l4

J3=l1*l2*l3+l2*l3*l4+l1l3l4+l1l2l4

J4=l1l2l3l4.

После того, как собственные числа найдены для каждого из них определяются собственные векторы.

Обратные матрицы.

Матрица В называется обратной по отношению к А, если выполняется равенство:

А*В=В*А=Е

В=А^-1;  (1)

Способы нахождения обратной матрицы.

Из (1) следует свойство обратной матрицы:

det(A^-1*A)=det A^-1*det A=det E=1

det A^-1=1/det A

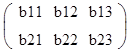
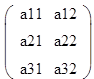Определитель определён для квадратной матрицы. Существуют методы построения А^-1 так же относящиеся к квадратной матрице, хотя определение не запрещает существования обратной матрицы для случая, когда число строк не равно числу столбцов.

=С

3*3

А=В^-1;

A*x=y