Методические указания по выполнению лабораторных работ по дисциплинам «Вычислительные сети» и «Информационные технологии проектирования электронных средств», страница 12

Для каждой таблицы R_i составляется минимальная строка, в которую заносятся значения минимальных элементов каждого столбца. Минимальной строке присваивается номер УК, на котором эта строка формируется.

На каждом этапе преобразования таблиц рельефов строки исходных таблиц заменяются соответствующими им по номеру минимальными строками, каждый элемент которых предварительно увеличен на длину ветви, связывающей рассматриваемые соседние узлы. Затем вновь определяются минимальные строки. Процесс формирования таблиц завершается, когда ни одна минимальная строка, полученная на очередном шаге, не будет отличаться от соответствующей минимальной строки, полученной на предыдущем шаге.

Таблицы рельефов идентичны дистанционным таблицам, полученным матричным методом.

3 Пример нахождения кратчайшего пути по матричному методу

Пусть структура сети задана (см. рисунок 1). Длина ветви (канала связи) между двумя любыми соседними УК для упрощения расчета принимается равной единице. Тогда длина пути будет измеряться числом транзитных участков. Исходная матрица длин ветвей L имеет вид:

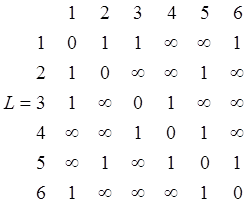
Определим матрицу   L¹ путем умножения L самой насебя с заменой операции умножения на сложение, а операции сложения на выбор минимума и с подстановкой полученных результатов в исходную матрицу длин L.

Определим элементы .

Так как , то замены в матрице L нет.

Так как  и , то замены в матрице L нет.

В матрице L элемент I_i4 заменяется на элемент , т.е.

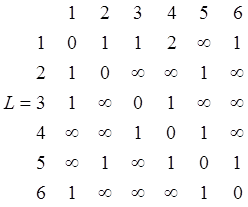
В матрице L элемент I_i5 заменяется на элемент .

В матрице L замены нет.

……   ……      ……..    ………     ………..

Пересчитав остальные элементы I_ij, получим матрицу L¹, которая имеет вид

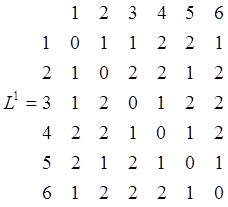
Теперь определим матрицу длин кратчайших путей U, умножив матрицу L¹ саму на себя, но в обратном порядке, начиная с элемента  по строке справа налево и по столбцу снизу вверх, с подстановкой полученных элементов в матрицу L¹:

………….   ………… ………… ………. ………. ……….

После всех расчетов матрица U имеет вид

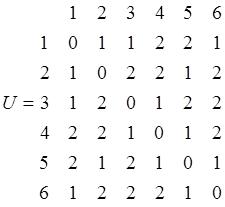
Рассмотрим пример построения дистанционной таблицы для УК₁. Длины путей между УК₁ и другими УК_i, i= будут зависеть от того, по какому пути передаются сообщения.

От УК₁ до УК₂ сообщение может передаваться по трем направлениям . Если сообщение к УК₂ передается по направлению УК₁ – УК₂, то длина пути . Если сообщение к УК₂ передается по направлению УК₁ – УК₃, то длина пути . Если сообщение будет послано к УК₂ , т.е.  передается по направлению УК₁ – УК₆, то длина пути .

Для УК₁ дистанционная таблица имеет вид:

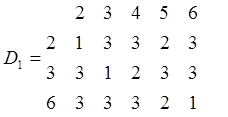
Для УК дистанционная таблица имеет вид:

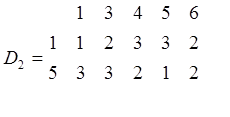
Выбор направлений передач по элементам дистанционных таблиц осуществляется следующим образом. Пусть требуется передать сообщение от УК₁ к УК₄. в таблице D₂ в столбце, соответствующем УК₄, выбирается минимальный элемент (2) и определяется строка (вторая),  которой принадлежит выбранный элемент. Указанная строка принадлежит соседнему с УК₂ узлу 5, поэтому в первую очередь следует пытаться направить сообщение к УК₅, а во вторую – к УК_i.

Маршрутные таблицы для УК₁ к УК₂ будут иметь следующий вид:

 , 

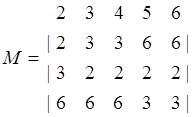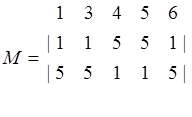
Каждый столбец маршрутной таблицы M_i (М₂) содержит соседние с УК₁ (УК₂) узлы сети, упорядоченные в соответствии с очередностью выбора направлений. Если несколько путей имеют одинаковую длину, то при выборе направления могут учитываться любые другие факторы (емкость, надежность, достоверность и т.д.).

4 Пример нахождения кратчайшего пути по методу рельефов

Рассмотрим построение рельефов для сети.

Длина всех ветвей принимается равной единице.

Исходные таблицы рельефов и соответствующие им минимальные строки имеют следующий вид.

Шаг 0.

;           ;

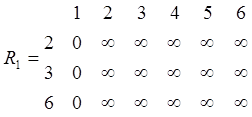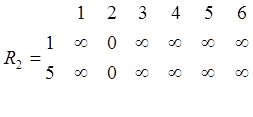min 1=[0 ¥ ¥ ¥ ¥ ¥];                                  min 2=[ ¥ 0 ¥ ¥ ¥ ¥];

;            ;

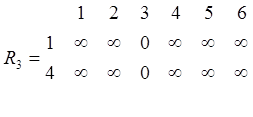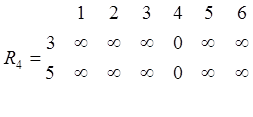min 3=[ ¥  ¥  0 ¥ ¥ ¥];                               min 4=[ ¥  ¥   ¥ 0 ¥ ¥];

;              ;

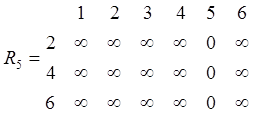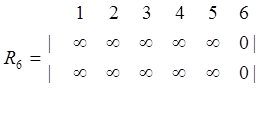min 5=[ ¥  ¥   ¥ ¥ 0 ¥];                              min 6=[ ¥  ¥   ¥  ¥ ¥ 0].

Строки исходных таблиц рельефов заменяются соответствующими им по номеру минимальными строками, каждый элемент которых предварительно увеличен на длину ветви, связывающей рассматриваемые соединения УК. Результаты будут следующие.

Шаг 1.

;           ;

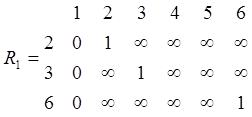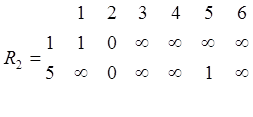min 1=[0 1 1 ¥ ¥ 1];                         min 2=[ 1 0 ¥ ¥ 1 ¥];