Методические указания по выполнению лабораторных работ по дисциплинам «Вычислительные сети» и «Информационные технологии проектирования электронных средств», страница 11

Определение длины кратчайшего пути основано на утверждении о том, что если кратчайший путь m(i,N) от произвольного УК_i и УК_N проходит через промежуточные ,... , , то кратчайшие пути m(x_i,N), m(x₂,N), … , m(x_k,N) от   к УК_N являются частями кратчайшего пути m(i,N). На рисунке 3 приведена иллюстрация данного утверждения.

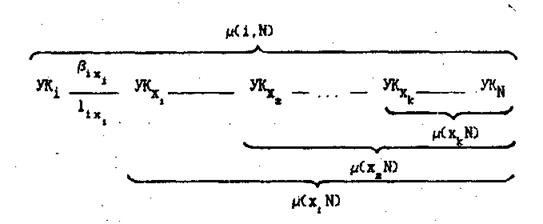
Рисунок 3

(1)

Если - ветвь, соединяющая УК_i и , a  - длина этой ветви, то длина кратчайшего пути U_iN определяется:

  .                         

(2)

По определению m(i,N) - самый короткий путь от УК_i  к УК_N, следовательно,

   j=1,2,…,x_i,…,n,

где n - число УК в сети. Таким образом, процедура определения U_iN для всех УК_i при заданном N и U_NN=0 является итеративной и решается методами динамического программирования.

(3)

Процедура определения кратчайшего пути от УК_i  к УК_N сводится к поочередному сравниванию и   выбору   минимального   из   путей,    в   зависимости от имеющегося в них числа промежуточных УК.

,   ,

(4)

Затем выбирается   минимальный   из путей,    имеющий один промежуточный узел,

,  , ,

(5)

и т.д. до выбора минимального из путей, имеющих  р-1 промежуточных УК, т.е.

,  , , , для всех р=1,n-1.

Просматривая поочередно значения величины  и выбирая минимальные для всех значений , , , можно получить длины кратчайших путей между всеми УК сети.

Рассмотрим матричный метод определения длины кратчайшего пути. Длина кратчайших путей между УК сети определяется возведением в степень  матрицы длины ветвей L. Алгоритм получения L^Р реализуется как последовательное (р-1) - кратное умножение матрицы L самой на себя

L^P=LL^P-1

Пусть , где  - элемент i-ой строки и х-го столбца, . По правилам умножения матриц элемент  матрицы L^P определится

                  (6)

В алгоритме получения кратчайших путей операция умножения заменяется операцией сложения, а операция сложения - операцией выбора минимума.  Уравнение (6)   запишется в виде

.                               (7)     

При j=N следует, что , так как

;                                                                     (8)

.                                                                   (9)

Для уменьшения трудоемкости алгоритма, после вычисления каждого элемента произведения матриц полученное значение вносится в исходную матрицу взамен соответствующего элемента этой матрицы. Это позволяет при вычислении каждого элемента произведения двух матриц использовать значения всех элементов, вычисленных ранее.

Для определения длины кратчайших путей между всеми парами УК сети достаточно только дважды умножить исходную матрицу длин саму на себя, с подстановкой в эту матрицу вычисляемых элементов. Первый раз элементы произведения матриц вычисляются, как обычно, по строкам сверху вниз, а внутри строк - слева направо, а второй раз в обратном порядке - по строкам снизу вверх, а внутри строк - справа налево. Таким образом, в результате работы алгоритма будет получена матрица , где элемент u_ij  определяет длину минимального пути от УК_i  к УK_j.

Из матриц L и U определяют длину путей между УК_i  и УK _j строят дистанционные таблицы, в которых каждый столбец  сопоставлен конечному УК, а каждая строка - УК, соседнему с начальным УК пути. Элементы дистанционной таблицы используются для распределения сообщений. Если в дистанционной таблице упорядочить направления к соседним УК в той последовательности, в которой они должны выбираться (исходя из увеличения пути), то получим таблицу, называемую маршрутной. Примеры построения дистанционной и маршрутной таблиц приведены ниже.

Рассмотрим определение длины кратчайшего пути по методу рельефов. В указанном методе "N - рельефом" называется набор весов всех ветвей, определенных для фиксированного УК. Рельефы сети записываются в специальные таблицы рельефов.

На каждом УК_i составляется исходная таблица рельефов R_i. Число столбцов таблицы определено числом УК в сети, а число строк - числом ветвей, исходящих из УК, для которого эта таблица составлена. Столбцам присваиваются номера УК, а строкам - номера УК, с которыми осуществлено соединение по ветви. В исходных таблицах R_i все элементы, кроме элементов i-го столбца, принимается равными сколь угодно большой величине, а элементы i-го столбца принимаются равными нулю и в процессе преобразований таблицы не меняются.