Министерство образования РФ
Санкт- Петербургский государственный горный институт им. Г.В. Плеханова
(технический университет)
Кафедра общей и технической физики.
ЛАБОРАТОРНАЯ РАБОТА № 2
«ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ В ПРОСТОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ»
САНКТ-ПЕТЕРБУРГ
2003 г.
Цель работы. Исследование зависимостей периода колебаний от индуктивности и ёмкости. Изучение зависимости добротности контура от активного сопротивления.
Общие сведения.
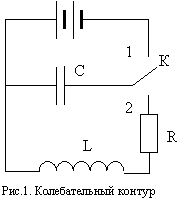
![]()
![]() Электрический колебательный
контур состоит из ёмкости С, индуктивности L и активного
сопротивления R (рис.1). Когда переключатель К поставлен в положение
1, батарея Е сообщает конденсатору некоторый заряд q. При
перебрасывании переключателя в положение 2 конденсатор начинает разряжаться
через катушку, в цепи возникает Э.Д.С. самоиндукции, под действием которой
конденсатор разряжается не мгновенно и после разрядки его до нуля ток в контуре
не прекращается, а продолжает протекать в прежнем направлении в течение
некоторого времени, вследствие чего на обкладках конденсатора появляется заряд,
противоположный начальному по знаку. Таким образом, конденсатор оказывается
перезаряженным, и в контуре вновь протекает процесс его разрядки, но в обратном
направлении. Такие периодические изменения зарядов, напряжений и токов в
контуре носят название электромагнитных колебаний. При этом происходит
непрерывный переход энергии электрического поля в конденсаторе в энергию
магнитного поля в катушке и обратно. В некоторый момент времени полная энергия
колебаний:
Электрический колебательный
контур состоит из ёмкости С, индуктивности L и активного
сопротивления R (рис.1). Когда переключатель К поставлен в положение
1, батарея Е сообщает конденсатору некоторый заряд q. При
перебрасывании переключателя в положение 2 конденсатор начинает разряжаться
через катушку, в цепи возникает Э.Д.С. самоиндукции, под действием которой
конденсатор разряжается не мгновенно и после разрядки его до нуля ток в контуре
не прекращается, а продолжает протекать в прежнем направлении в течение
некоторого времени, вследствие чего на обкладках конденсатора появляется заряд,
противоположный начальному по знаку. Таким образом, конденсатор оказывается
перезаряженным, и в контуре вновь протекает процесс его разрядки, но в обратном
направлении. Такие периодические изменения зарядов, напряжений и токов в
контуре носят название электромагнитных колебаний. При этом происходит
непрерывный переход энергии электрического поля в конденсаторе в энергию
магнитного поля в катушке и обратно. В некоторый момент времени полная энергия
колебаний:
![]() ,
,
где U и i - мгновенные значения разности потенциалов и тока. В те моменты времени, когда конденсатор полностью разряжен (U=0), ток достигает максимального значения Im, и полная энергия контура равна энергии магнитного поля:
![]()
Полная энергия колебаний постепенно уменьшается, так как электрическая энергия благодаря сопротивлению R непрерывно превращается в тепловую и рассеивается в окружающее пространство.
Составим дифференциальное уравнение колебаний в
контуре. Пусть q - мгновенное значение заряда на обкладках
конденсатора и U - разность потенциалов между обкладками в тот же
момент времени. Тогда полное напряжение в цепи ![]() равно
сумме действующих ЭДС. Так как в цепи действует только ЭДС самоиндукции:
равно
сумме действующих ЭДС. Так как в цепи действует только ЭДС самоиндукции:
![]() ,
,
![]() .
.
Подставив в это равенство значения ![]() ,
, ![]() получим:
получим:
![]() , (1)
, (1)
Разделим обе части уравнения (1) на L и введём обозначения:
![]() ,
(2)
,
(2)
![]() (3)
(3)
где величина a называется коэффициентом затухания; w0 – собственная частота колебаний контура. Тогда дифференциальное уравнение колебаний примет вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.