Экспериментальное определение коэффициента теплопроводности и удельного сопротивления металлов, проверка закона Видемана-Франца

Санкт-Петербургский государственный горный институт

(технический университет)

Кафедра общей и технической физики

Лаборатория физики твердого тела и квантовой физики

Лабораторная работа 7

Исследование тепло- и электропроводности металлов

Санкт-Петербург

2008

Цель работы – экспериментальное определение коэффициента теплопроводности и удельного сопротивления металлов, проверка закона Видемана-Франца.

Общие теоретические сведения

В металле атомы расположены близко друг от друга, потенциальные барьеры между соседними атомами снижены, электроны получают возможность туннелировать через эти барьеры, т.е. перемещаться от атома к атому, теряя свою принадлежность тому или иному атому. Поэтому металл можно представить как коллектив электронов и коллектив атомных остовов.

Такое перемещение электронов сложно описать, однако, учитывая, что в идеальной кристаллической решетке электроны практически не испытывают рассеяния при движении, можно сделать упрощение - считать электроны газом свободных частиц, имеющими эффективную массу m*. Электроны имеют спин 1/2 и подчиняются статистике Ферми-Дирака. Поэтому каждое разрешенное энергетическое состояние может быть занято только двумя электронами в соответствии с принципом Паули. Следствием этого является распределение частиц по энергиям, которое в случае металлов приводит к отсутствию запрещенной зоны или к неполному заполнению разрешенной зоны. Уровень Ферми располагается внутри зоны. При Т=0 К все уровни ниже уровня Ферми заняты, а уровни выше уровня Ферми свободны. При T>0 K кристалл получает энергию порядка kT, за счет этого возбуждения некоторые электроны, находящиеся вблизи уровня Ферми E_F, начинают заполнять состояния с более высокой энергией. Концентрация <n_эл>свободных электронов в металле слабо зависит от температуры, так как положение уровня Ферми практически не зависит от температуры. Она равна:

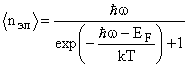
Электронный газ в металлах является вырожденным, т.е. подчиняется статистике Ферми-Дирака, вплоть до температур ~10⁴ К. Вследствие этого в процессах переноса могут принимать участие не все свободные электроны, а только небольшая их часть, имеющая энергию, близкую к энергии Ферми. Соответственно и скорости движения электронов мало отличаются от скорости, соответствующей энергии Ферми v_F.

Атомные остовы, образующие правильную кристаллическую решетку, совершают колебательные движения вблизи положений равновесия. В трехмерной кристаллической решетке возможны многие виды колебаний с различными частотами.  Согласованные движения большого коллектива атомов также как и в случае электронов удобно описывать, вводя квазичастицы. Каждому колебанию сопоставляют квазичастицу – фонон. Возникновение колебаний эквивалентно «рождению» фонона, а прекращение колебаний – «уничтожению» фонона. Колебания решетки распространяются со скоростью звука, поэтому v_фон = v_зв. Существует максимальная частота колебаний кристаллической решетки ω_D, которая носит название частоты Дебая. Ей можно сопоставить температуру Дебая Θ: , где k – постоянная Больцмана. Для меди Θ_Cu = 335 К, а для алюминия Θ_Al = 419 К.

Фононы имеют целый спин и подчиняются статистике Бозе - Эйнштейна, поэтому средняя концентрация фононов с энергией ħω при температуре Т равна

.

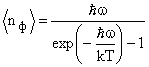При kТ>>ħω знаменатель упрощается  и средняя концентрация фононов пропорциональна температуре: ~<n> ~ T. При Т>Θ практически все фононы рождаются с максимальной энергией ħω_D.