1. Рассеяние
При T>Θ, учитывая зависимости ℓэл и n от температуры в этом диапазоне температур, для удельного сопротивления металла, обусловленного рассеянием на фононах, получим линейную зависимость ρф от температуры:
.
Импульс фононов при этом достаточно велик, чтобы обеспечить изменение импульса электрона от pF до нуля: ∆pэл ≈ pэл ≈ pф = kΘ/vзв.
При T<Θ эта зависимость нарушается. При понижении температуры рождается все меньше фононов, их энергии становятся все меньше. Импульс фонона мал и его недостаточно для остановки электрона, т.к. изменение импульса электрона не может превышать импульс фонона. Нужны многократные столкновения с фононами, прежде чем импульс электрона сможет заметно измениться. Кроме того, уменьшаются амплитуды колебаний атомов, а соответственно и эффективное сечение рассеяния. Теоретический расчет показывает в этой области степенную зависимость удельного сопротивления от температуры : ρф ~ T5 . Экспериментальные значения показателя степени лежат в пределах от 4 до 6. Температурный интервал, в котором наблюдается такая зависимость, обычно очень небольшой.
Сопротивление, обусловленное рассеянием на дефектах, ρост не зависит от температуры и называется остаточным сопротивлением.
2. Электропроводность в широком диапазоне температур
Для металлов справедливо правило Матиссена: полное сопротивление металлов суть сумма сопротивления, обусловленного рассеянием электронов на тепловых колебаниях решетки (фононах), и остаточного сопротивления, обусловленного рассеянием на статических дефектах структуры ρ = ρф + ρост. Исключение из этого правила составляют сверхпроводящие металлы, в которых остаточное сопротивление равно нулю и полное сопротивление исчезает ниже некоторой критической температуры.
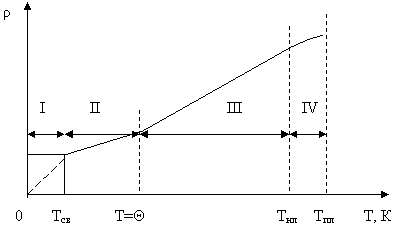
Рис. 1. Зависимость удельного сопротивления металла от температуры.
В зависимости удельного сопротивления металла от температуры в широком диапазоне температур (рис. 1) можно выделить несколько характерных участков:
I – наблюдается сверхпроводимость у чистых металлов и остаточное сопротивление у металлов с дефектами;
II – переходная область с сильной степенной зависимостью ρ ~ Tm , где показатель степени убывает от m=5 до m=1 при T=Θ;
III – линейный участок, у большинства металлов простирается до температур, порядка ⅔Θ, т.е от комнатных до близких к точке плавления;
IV – вблизи точки плавления начинается отклонение от линейной зависимости, вызванное ангармоничностью колебаний кристаллической решетки.
В области линейной зависимости удельного сопротивления от температуры справедливо выражение ρ = ρ0[1+α(T-T0)], где Т0 – начальная температура, ρ0 – удельное сопротивление при Т0, α – температурный коэффициент удельного сопротивления, показывающий насколько изменяется удельное сопротивление при изменении температуры на один Кельвин.
III. Закон Видемана-Франца.
Рассмотрим отношение удельной теплопроводности к удельной электропроводности при заданной температуре:
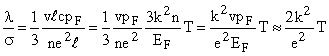
Аккуратный расчет показывает, что множитель 2 в этой формуле надо заменить на π3/3. Тогда
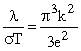
Это выражение называется законом Видемана-Франца, который справедлив при T>Θ, а постоянная величина
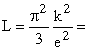2,45·10-8 В2/К2.
не зависит от природы металла и называется числом Лоренца.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.