Модульна контрольна робота з дисципліни «Вища математика» (Приклад)

Приклад

Модульна контрольна робота

з дисципліни «Вища математика»

студента групи  ___БСз ________________________________________________

Кожне тестове завдання оцінено в 2 бали.

1.  При якій умові можна для розв’язання квадратної лінійної системи застосовувати правило Крамера? Відповідь: а) основний визначник системи не дорівнює нулю;  б) основний визначник системи дорівнює нулю;  в) інше.

2.  Скалярний добуток двох векторів є     а) вектором   ; б) числом;    в) невизначеністю.

3.  Який геометричний об’єкт визначає рівняння ? Відповідь: а) площину;    б) пряму;          в) пряму в просторі.

4.  Правило Лопіталя застосовують у випадку невизначеностей вигляду: а)  або ; б) ; в)

5.  Якщо похідна функції приймає додатні значення в деякому інтервалі, то функція в цьому іптервалі  а) спадає;      б) опукла;         в) зростає.

6.  Маргінальна вартість – це економічний зміст а) похідної; б) інтеграла; в) границі.

7.  Площу криволінійної трапеції можна обчислити за допомогою:  а) похідної; б) визначеного інтеграла; в) границі.

8.  Якщо диференційовна функція f(x,y) має екстремум в деякій точці, то ії частинні похідні в цій точці а) додатні;  б) дорівнюють нулю; від’ємні.

9.  Рівняння вигляду  =f(x)g(y)  є диференціальним рівнянням 1-го порядку  а) з відокремлюваними змінними;  б) однорідним;  в) лінійним.

10.При почленному інтегруванні або диференціюванні збіжного степеневого ряду його радіус збіжності а) не змінюється; б) збільшується; в) зменшується.

Кожне завдання оцінено в 5 балів

1. Знайти невизначені інтеграли :

а)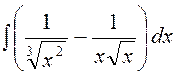

2. Обчислити визначений інтеграл :

а)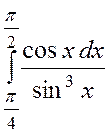                                   

3. Обчислити площу фігури, обмежену лініями :

                і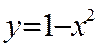        

4.  Розв’язати задачу економічного змісту:

Функція маргінального прибутку підприємства має вигляд 70-0,2x (у гривнях), де  - кількість одиниць продукції. Знайти зміну загального прибутку, якщо виробництво зросте з 1 до 20 одиниць.

5. Знайти похідну даної функції в точці А за даним напрямом :

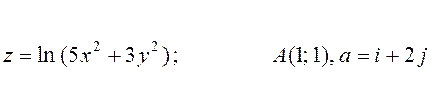
6. Дослідити на екстремум функцію двох змінних: