Методичні рекомендації та завдання до індивідуальної роботи № 1 з дисципліни «Вища математика»

Якщо визначник системи не дорівнює нулю, то система має єдиний розв’язок, який знаходиться за формулами

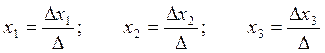
Обчислення визначників третього порядку виконується за допомогою правила трикутника

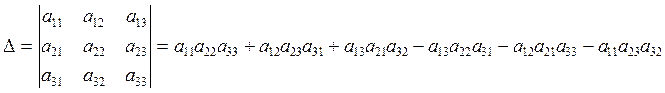
або розкладанням за елементами будь-якого рядка або стовпця: визначник дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їх алгебраїчні доповнення

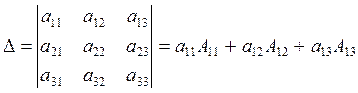
(розкладання за елементами першого рядка)

Алгебраїчне доповнення елемента    а_ij   визначається за формулою

Мінор  елемента  матриці n-го порядку – це визначник матриці (n-1) порядку, який одержується викресленням і-го рядка і j-го стовпця, на перетині яких знаходиться елемент.

Наприклад, обчислимо визначник

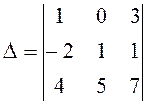
а) за правилом трикутника:

 = 1 · 1 · 7 + 0 · 1 · 4 + (-2) · 5  · 3 – 4 · 3  ·1 – 7 · (-2)  · 0 – 1 ·1  · 5 =  - 40 ;

б) розкладанням за елементами першого рядка:

а₁₁ = 1;     А₁₁  =  (-1)¹⁺¹ · 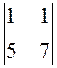    = 1· (7 - 5) = 2 ;

а₁₂ = 0;     А₁₃  =  (-1)¹⁺¹ · 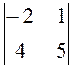    = 1· (-10 - 4) = -14 ;

 = 1 · 2 + 0 + 3 · (-14) = - 40.

Приклад 1. Розв’язати систему лінійних рівнянь за правилом Крамера.

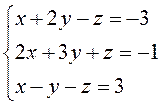
Складемо матрицю системи рівнянь, обчислимо визначник системи та додаткові визначники:

 

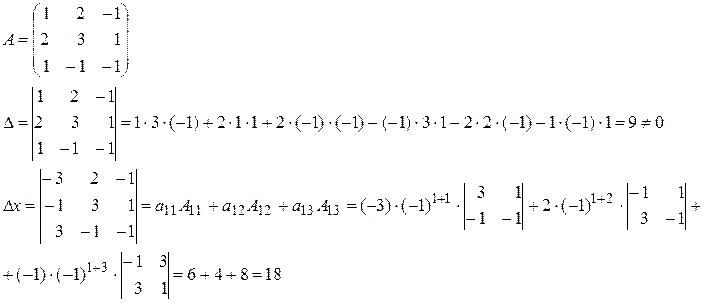
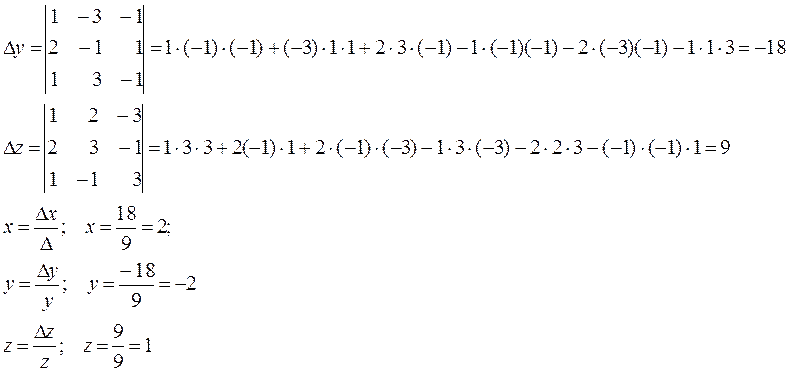
Відповідь: х = 2 ; y = 2 ; z = 1.

2. Розв’язання систем лінійних рівнянь за допомогою оберненої матриці.

Література: [1], с.104-106;  [3], с.81-89.

Розглянемо систему рівнянь (1) у матричному вигляді:

, де .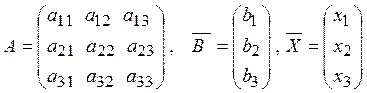

Розв’язок цієї системи за допомогою оберненої матриці знаходиться за формулою:

, де А^-1 – матриця, обернена до матриці А.

Для того, щоб квадратна матриця мала обернену, необхідно і достатньо, щоб визначник матриці не дорівнював нулю. Щоб знайти матрицю, обернену до даної, необхідно обчислити визначник матриці і алгебраїчні доповнення всіх елементів матриці; скласти матрицю із алгебраїчних доповнень елементів, транспонувати її (таким чином одержуємо союзну матрицю) і скористатися формулою

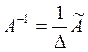
де   - визначник матриці А,   - союзна матриця.

Приклад 3. Розв’язати систему лінійних рівнянь, подану в прикладі 1, за допомогою оберненої матриці.

При розв’язуванні попереднього прикладу ми склали матрицю системи А і обчислили визначник . Визначник матриці А не дорівнює нулю, тому матриця А має обернену. Обчислимо алгебраїчні доповнення всіх елементів матриці:

,

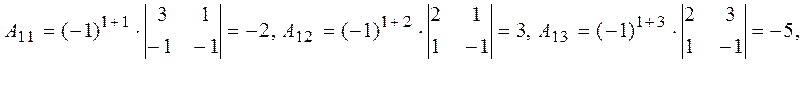
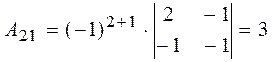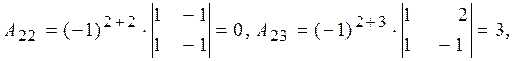
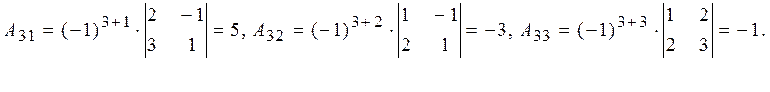
Складемо союзну матрицю:

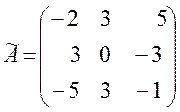
Знайдемо обернену матрицю

.

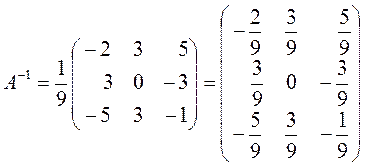Тоді

  .

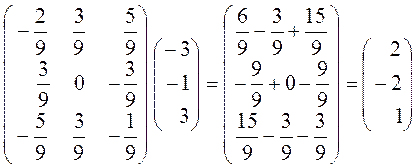Відповідь:

3. Розв’язання систем лінійних рівнянь методом Гаусса.

Література: [1], с.107-110; [2], с.29-33; [3], с.101-104.

При розв’язуванні систем лінійних рівнянь методом Гаусса використовується наступний алгоритм. Можна вважати, що коефіцієнт при х₁ у першому рівнянні відмінний від нуля (у противному випадку слід поміняти місцями перше рівняння і рівняння, в якому коефіцієнт при х₁ відмінний від нуля). Ділимо перше рівняння на коефіцієнт при х₁. В результаті коефіцієнт при х₁ у першому рівнянні буде рівним одиниці. Із другого рівняння віднімаємо перше рівняння, помножене на коефіцієнт при х₁ у другому рівнянні. Із третього рівняння віднімаємо перше, помножене на коефіцієнт при х₁ у третьому рівнянні. Повторюючи цю процедуру для всіх рівнянь, починаючи з другого, виконуємо виключення невідомого х₁ з усіх рівнянь. Розглянемо одержану таким чином систему рівнянь. Можна вважати, що коефіцієнт при х₂ у другому рівнянні відмінний від нуля. Ділимо друге рівняння на коефіцієнт при х₂ у другому рівнянні. В результаті коефіцієнт при х₂ у другому рівнянні буде дорівнювати одиниці. З третього рівняння віднімаємо друге, помножене на коефіцієнт при х₂ у третьому рівнянні. В результаті з третього рівняння виключаємо невідоме х₂. Повторюємо цю процедуру для всіх наступних рівнянь. Далі виключаємо невідоме х₃ з усіх рівнянь, починаючи з четвертого і т.д. Звертаємо увагу на те, що за допомогою методу Гаусса можна розв”язувати будь-яку систему лінійних рівнянь (не обов'язково квадратну, з будь-яким визначником системи).

Приклад 4.

1. Розв’язати систему лінійних рівнянь, подану у прикладі 1, методом Гаусса:

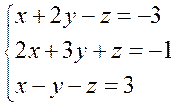
Виключаємо невідоме х із другого і третього рівнянь

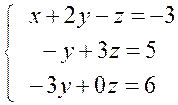
y= – 2

3 z = 5 + y; 3z = 3; z = 1

x = – 3 – 2y + z; x = – 3 – 2 (–2) + 1 = 2

Таким чином, x = 2, y = -2, z = 1.

Відповідь: x = 2, y = -2, z = 1.

Приклад 5. Розв’язати систему лінійних рівнянь методом Гаусса:

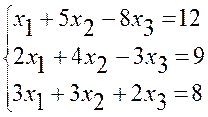
Виключаємо невідоме х₁ із другого і третього рівнянь

Ділимо друге рівняння на (-6) і виключаємо невідоме х₂ з третього рівняння

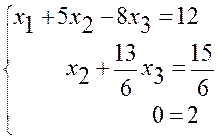
Розглянувши третє рівняння, робимо висновок, що система рівнянь не має розв’язків (система лінійних рівнянь несумісна).

Приклад 6. Розв’язати систему рівнянь методом Гаусса

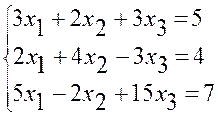
Ділимо перше рівняння на 3 і виключаємо невідоме х₁ з другого і третього рівнянь 

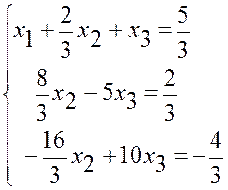
Ділимо друге рівняння на  і виключаємо х₂ з третього рівняння