Завдання міжвузівської студентської математичної олімпіади

Завдання міжвузівської студентської математичної олімпіади

1. Розв’яжіть нерівність  .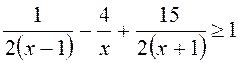

Розв’язання

Перенесемо 1 в ліву частину нерівності і приведемо  до спільного знаменника:

;

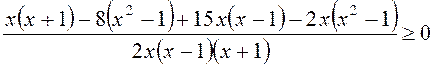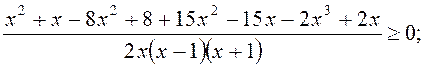
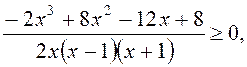  или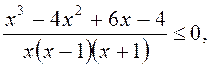 

чисельник розкладається на множники

Нерівність прийме вигляд:

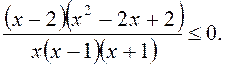                                                 (1)

Дискримінант тричлена менше нуля. Отже, при будь-яких значеннях   х тричлен додатній.  Тому нерівність (1) рівносильна нерівності

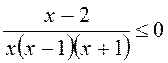.                                                            (2)

Тут х≠ 0;   х≠1;    х≠–1.

Помножимо обидві частини нерівності (2) на додатне  число . Одержимо

                                                (3)

Корені виразу, що стоїть в лівій частині нерівності (3), суть 2; 1; 0; –1.

Правіше за найправішого кореня вираз додатній, між 1 і 2 – від’ємний, в інтервалі від 0 до 1 – додатній, від 0 до –1 – від’ємний і при  х <–1 – додатній.

Таким чином, нерівності задовольняють значення х в межах:

2. Знайти функцію у(х), що має постійну еластичність k.

Розв’язання

За умовою задачі маємо . Отже,

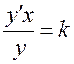, тобто .

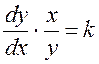Звідси, при природному припущені, що х ≠0, одержимо:

.

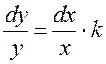Інтегруючи обидві частини отриманої рівності, знайдемо:

.

Не втрачаючи загальності, подамо цю рівність у вигляді:

 або .

Потенціюючи останнє співвідношення, одержимо вигляд функції, що має постійну еластичність, яка дорівнює k:  у=Сх^k.

3. Скількома способами можна розміняти 20 копійок на монети вартістю в 5, 2 і 1 копійку?

Відповідь:  Існує 29 способів такого розміну.

4. На площині дані 4 точки A, B, C, D, що є вершинами опуклого чотирикутника. Довести, що точки перетину медіан трикутників ABC,  ABD,  ACD,  BCD є вершинами чотирикутника, подібного даному.

Підказка . 1. Скористайтеся основною властивістю медіан трикутника і покажіть, що сторони нового трикутника паралельні сторонам даного.

2. Обчисліть вектори, що йдуть з точки О  перетину середніх ліній чотирикутника ABCD  до центрів тяжіння вказаних трикутників, і використайте рівність

5. Знайти хоча б одне значення х з інтервалу 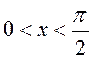, при якому одно з чисел sinx, sin2x, sin3x є середнім арифметичним двох інших. Відповідь обґрунтуйте.

Розв’язання

Покажемо, як знайти таке х, для якого 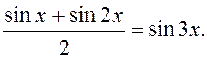. Оскільки

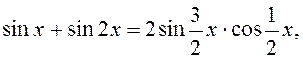
то рівність 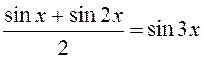 рівносильна

.

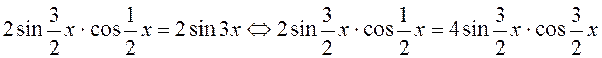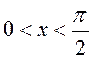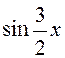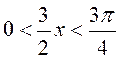На інтервалі   функція  не повертається в 0 (оскільки ). Тому остання рівність рівносильна .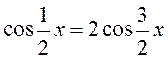

Використовуючи формулу косинуса потрійного кута  , одержуємо, що остання рівність рівносильна

.

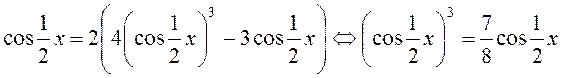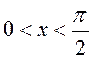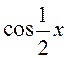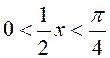На інтервалі    функція  не повертається в 0 (оскільки ). Тому остання рівність рівносильна

.

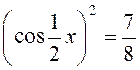Це рівняння має розв’язання 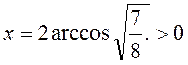. Покажемо, що число  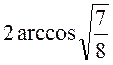належить інтервалу 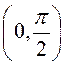. Оскільки 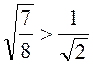, а arcos  - функція, що убуває,  то

.

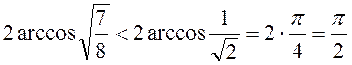Отже, при 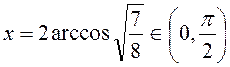 число sin3x є середнім арифметичним чисел sinx і sin2x.

6. Знайти всі функції f: R→R, які задовольняють тотожності

.

Покладемо в початковій тотожності x=y=1, тоді одержимо  тобто f(1)=0  або f(1)=1. Розглянемо кожний з цих випадків:

а) Якщо f(1)=0, то поклавши в тотожності y=1, одержимо тотожність f(1)=0.

б) Якщо f(1)=1, то знову поклавши в тотожності y=1, одержимо тотожність

 тобто , з цього при будь-якому х≠0 маємо f(1)=1. Таким чином, для функції f(х) маємо дві можливості: або f(х)=0, або

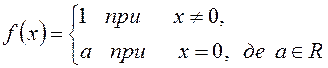
Перевірка показує, що будь-яка з цих функцій задовольняє умові задачі.

Довідниковий матеріал. 1) Еластичністю функції у=f(х) щодо змінної х називають границю відношення відносного збільшення у до відносного збільшення змінної х при :  .

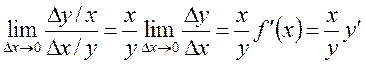2) Корисні тригонометричні формули:

.