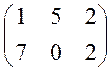Составление математической модели задачи и её решение симплекс-методом и графическим методом. Расчет оптимальной стратегии и цены игры, заданной платежной матрицей, страница 4

Прибавив ко всем элементам матрицы A’, например, число c=3, получим матрицу A’’, все элементы 1 строки которой строго положительны, а все элементы 2 строки неотрицательны.

A’’=

Составим пару симметричных двойственных задач, так чтобы исходная задача была стандартной задачей максимизации, матрица коэффициентов этой задачи совпадала с платежной матрицей A’’, а коэффициенты при неизвестных в целевой функции и свободные члены неравенств были бы равны единице.

Задача 1.                                                       Задача 2.

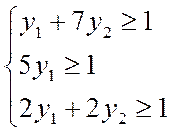
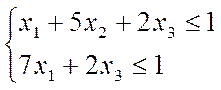
     Решим задачу 1 симплекс-методом. Она задана в форме общей задачи. Сведем ее к основной при помощи дополнительных переменных   и прибавим их к левым частям неравенств (I), тогда получим основную задачу:

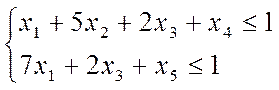
Эта задача является канонической и, применив к ней алгоритм симплекс-метода, получим симплексные таблицы вида.

Из столбца x₀ и индексной строки Табл.4 выпишем оптимальные планы пары двойственных задач: X*=(0,0,0.5), Y*=(0.2, 0.3), причем f(X*)=f(Y*)=0.5.

Из решения пары двойственных задач получим цену игры и оптимальные стратегии игроков: v’’=1/f(X*)=1/f(Y*)=2, P’*=v’’Y*=(0.4,0.6), Q’*=v’’X*=(0,0,1).

Игра с матрицей A’ будет иметь те же оптимальные стратегии P’* и Q’*? Что и игра с матрицей A’’, причем цена игры будет v’=v’’-c=2-3=-1.

И наконец, исходная игра A имеет оптимальные стратегии игроков P*=(0, 0.4, 0.6), Q*=(0, 0, 0, 1) (полученные из стратегий P’* и Q’*, приписав нули на месте удаленных строк и столбцов) и цену игры v=v’=-1.

Проверим правильность решения игры с помощью критерия оптимальности стратегий. Для этого подставим компоненты найденных оптимальных стратегий P* и Q*, компоненты чистых стратегий P_i (i=1,2,3) и Q_j (j=1,2,3,4) в неравенство

И сравним их с ценой игры v=-1.

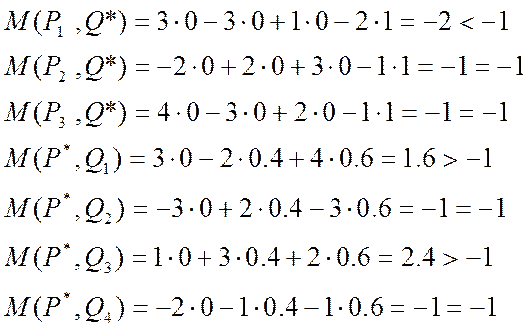
Мы видим, что все неравенства выполнены, значит, решение игры выполнено правильно.

Ответ: Игра A имеет оптимальные стратегии игроков P*=(0, 0.4, 0.6), Q*=(0, 0, 0, 1) (полученные из стратегий P’* и Q’*, приписав нули на месте удаленных строк и столбцов) и цену игры v=v’=-1.