1-20. Составить математическую модель задачи и решить ее двумя способами: симплекс-методом и графически. Для полученной задачи составить двойственную и проверить оптимальность плана исходной задачи с помощью критериев оптимальности планов двойственных задач.
Решение: Составить математическую модель по данной таблице:
|
Виды ресурсов |
Технолог. Способы I II |
Запасы ресурсов |
||
|
Сырье |
3 |
1 |
18 |
|
|
Трудовые ресурсы |
1 |
3 |
14 |
|
|
Накладные расходы |
1 |
2 |
6 |
|
|
Прибыль |
4 |
2 |
||
Составить план использования технологических способов в производстве, обеспечивающих максимальную прибыль.
Математическая модель задачи:
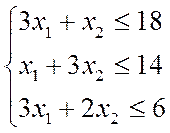 (I)
(I)
![]() (II)
(II)
![]() - целевая функция. (III)
- целевая функция. (III)
![]() Задача (I)-(III) является
общей задачей, т.к. система ограничений (I) состоит
из неравенств.
Задача (I)-(III) является
общей задачей, т.к. система ограничений (I) состоит
из неравенств.
Введем дополнительные неизвестные и прибавим их к левым частям неравенств (I), тогда получим основную задачу:
![]()
![]()
 (IV)-(VI)
(IV)-(VI)
Основная задача (IV)-(VI) является канонической и поэтому ее можно решить симплекс-методом.
1. Симплекс-метод.
Составим таблицу
|
Табл.1 |
||||||||
|
0 |
4 |
2 |
0 |
0 |
0 |
|||
|
Базис |
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
||
|
0 |
x3 |
18 |
3 |
1 |
1 |
0 |
0 |
|
|
0 |
x4 |
14 |
1 |
3 |
0 |
1 |
0 |
|
|
0 |
x5 |
6 |
3 |
2 |
0 |
0 |
1 |
|
|
f |
0 |
-4 |
-2 |
0 |
0 |
0 |
||
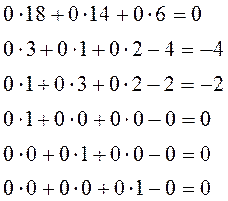 Последняя строка называется
индексной строкой, значения в которой находятся из следующих уравнений:
Последняя строка называется
индексной строкой, значения в которой находятся из следующих уравнений:
Обозначим: ключевая строка: s=3
ключевой столбец: r=1
Задача считается решенной, если все элементы индексной строки неотрицательны. У нас это условие не выполнено, это означает, что исходный базис можно улучшить, построив новую таблицу. По табл.1 базисный план X1=(0,0,18,14,6), для которого значение целевой функции f(X1)=0.
Чтобы построить новую таблицу, среди элементов индексной строки выберем наименьший элемент. В нашем случае он равен -4, который находится в столбце x1. Это означает, что неизвестный x1 вводится в базис. Осталось определить ключевую строку по формуле:
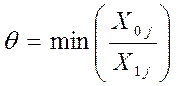
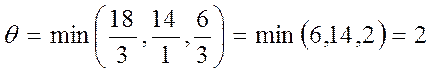 Поэтому,
Поэтому,
Это означает, что нас интересует 3 строка, поэтому строка с неизвестным x5 выводится из базиса. На пересечении ключевого столбца и ключевой строки стоит элемент 3 (в табл.1 выделен зеленым цветом).
Составим таблицу 2:
|
Табл.2 |
||||||||
|
0 |
4 |
2 |
0 |
0 |
0 |
|||
|
Базис |
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
||
|
0 |
x3 |
12 |
0 |
-1 |
1 |
0 |
-1 |
|
|
0 |
x4 |
12 |
0 |
|
0 |
1 |
|
|
|
4 |
x1 |
2 |
1 |
|
0 |
0 |
|
|
|
f |
8 |
0 |
|
0 |
0 |
|
||
Найдем значения:
3 строка: элементы 3-й строки из табл.1 разделили на ключевой элемент=3.
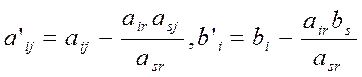 1 и 2 строки: вычисляются по
следующим формулам, где s=3, r=1.
1 и 2 строки: вычисляются по
следующим формулам, где s=3, r=1.
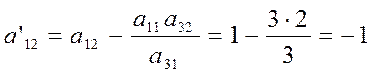 Например, покажем для элемента a12, остальные вычисляются
аналогично, подставляя в формуле нужные индексы.
Например, покажем для элемента a12, остальные вычисляются
аналогично, подставляя в формуле нужные индексы.
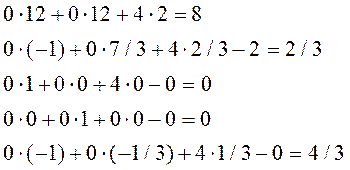 Значение индексной строки
вычисляются аналогично Табл.1.
Значение индексной строки
вычисляются аналогично Табл.1.
Получилось, что в индексной строке все элементы неотрицательны, значит, задача решена. Базисный план X2=(2,0,12,12,0), для которого f(X2)=8 – есть максимальное значение целевой функции. Значит, X2=(2,0,12,12,0) является оптимальным планом основной задачи (IV)-(VI). Обозначим его X2*=(2,0,12,12,0), тогда f(X2*)=8- максимальное значение целевой функции (VI).
Отбросив значение дополнительных переменных, получим:
Ответ: оптимальный план X*=(2,0) общей задачи (I)-(III), а значение целевой функции останется прежним f(X*)=8.
Таким образом, для того, чтобы получить максимальную прибыль, равную 8 ед., следует использовать 2ед. ресурсов I вида. Значения дополнительных неизвестных x3*=x4*=12 и x5*=0 показывают, что ресурсы I, II видов используются не полностью, а III вида – полностью.
2.Графический способ.
Общая задача (I)-(III) содержит 2 неизвестных, поэтому может быть решена графически.
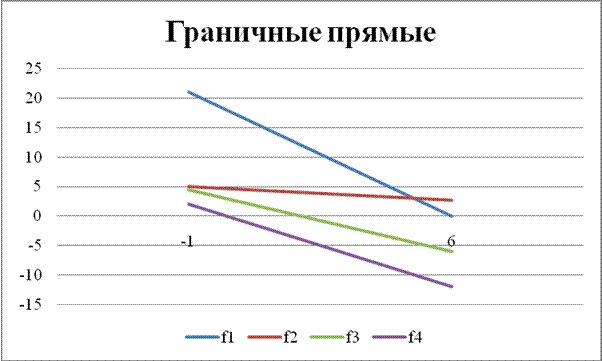
Введем систему декартовых координат на плоскости x1Ox2 и построим множество планов задача (I)-(III). Каждое линейное неравенство системы определяет полуплоскость по одну сторону от граничной прямой, заданной соответствующим равенством. Множество планов задачи есть пересечение полуплоскостей, представляющих собой выпуклый многоугольник.
![]()
![]() Построим каждую из граничных
прямых :
Построим каждую из граничных
прямых :
![]()
![]()
![]()
![]() Определим направление
полуплоскостей: так как каждое из неравенств (I)
содержит точку О(0,0):
Определим направление
полуплоскостей: так как каждое из неравенств (I)
содержит точку О(0,0):
![]() Поэтому полуплоскости обращены к
началу координат. Так как , то множество планов задачи (I)-(III)
представляет собой пересечение трех полуплоскостей, попавшее в I-ую координатную четверть, т.е многоугольник.
Поэтому полуплоскости обращены к
началу координат. Так как , то множество планов задачи (I)-(III)
представляет собой пересечение трех полуплоскостей, попавшее в I-ую координатную четверть, т.е многоугольник.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.