Составление математической модели задачи и её решение симплекс-методом и графическим методом. Расчет оптимальной стратегии и цены игры, заданной платежной матрицей, страница 3

Выберем , при включении в план X₁ перевозки

суммарная стоимость перевозок изменится на

, то есть уменьшится на 5, поэтому 

Пересчитав все перевозки, вошедшие в цикл плана при

Получим новый план перевозок X₂.

	5	8	3	u1=0
X2=	2	4	2	u2=1
	7	6	3	u3=3
	0	0	0	u4=-3
	v1=5	v2=3	v3=3

План X₂ лучше X_1, так как стоимость перевозок f(X₂)=210. Проверим план X₂ на оптимальность. Для занятых клеток составим систему:

u₁+v₁=5       u₂+v₂=4        u₄+v₂=0

u₁+v₃=3       u₃+v₂=6        u₄+v₃=0

Снова зададим u₁=0, отсюда получим, что   u₂=1, u₃=3, u₄=-3, v₁=5, v₂=3, v₃=3.

По условию 1⁰ для свободных клеток:

Подставив потенциалы, получим:

0+3=3 < 8    3+3=6 > 3   3+5=8 > 7

1+3=4 >2    1+5=6 > 2  -3+5=2 > 0

Мы видим, что не выполнено 5 неравенства из 6, причем,

.

Следовательно, план перевозок можно улучшить, введя перевозку

x₂₁= . С этой целью составим цикл, имеющий начало в клетке (2,1). В результате получим план

	5	8	3
X3(0)=	2	4	2
	7	6	3
	0	0	0

Выберем , при включении в план X₂ перевозки

суммарная стоимость перевозок изменится на

, то есть уменьшится на 36, поэтому 

Пересчитав все перевозки, вошедшие в цикл плана при

Получим новый план перевозок X₃.

	5	8	3	u1=0
X3=	2	4	2	u2=-3
	7	6	3	u3=-1
	0	0	0	u4=-7
	v1=5	v2=7	v3=3

План X₃ лучше X_2, так как стоимость перевозок f(X₃)=174. Проверим план X₃ на оптимальность. Для занятых клеток составим систему:

u₁+v₁=5       u₂+v₂=4        u₄+v₂=0

u₁+v₃=3       u₃+v₂=6        u₂+v₁=2

Снова зададим u₁=0, отсюда получим, что   u₂=-3, u₃=-1, u₄=-7, v₁=5, v₂=7, v₃=3.

По условию 1⁰ для свободных клеток:

Подставив потенциалы, получим:

0+7=7 < 8    -1+3=2 < 3   -1+5=4 < 7

-3+3=0 < 2    -7+3=-4 < 0  -7+5=-2 < 0

Отсюда следует, что выполняются оба условия 1⁰ и 2⁰ критерия оптимальности плана перевозок. Следовательно, план X₃ является оптимальным планом закрытой модели, а f(X₃)=174 представляет собой наименьшую стоимость перевозок.

Отбросив последнюю строку плана X₃, получим оптимальный план X* исходной открытой модели, для которой f(X*)=174 есть наименьшая стоимость перевозок. Отброшенная строка означает, что у второго потребителя останется недопоставлено 18 единиц продукции.

Ответ: оптимальный план X* исходной открытой модели, для которой f(X*)=174 есть наименьшая стоимость перевозок.

	5	8	3
X*=	2	4	2
	7	6	3

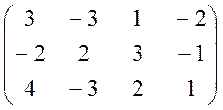41-60. Найти оптимальные стратегии и цену игры, заданной платежной матрицей А.

А =

Решение: 

Заметим, что в матрице А нет седловой точки, значит игра имеет решение в смешанных стратегиях.

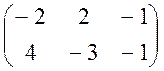Кроме того, первая строка доминируемая третей строкой, так как все элементы первой строки не больше соответствующих элементов третей строки, поэтому ее можно удалить. Также 3 столбец доминирует над 4 столбцом, поэтому его тоже можно удалить. А результате получим матрицу                        

A’ =