Составление математической модели задачи и её решение симплекс-методом и графическим методом. Расчет оптимальной стратегии и цены игры, заданной платежной матрицей, страница 2

Определим теперь вектор нормали n. Его координаты берем из целевой          функции n=(4,2). Строим перпендикуляр к нормали n – получим график целевой функции (на рисунке f₄). Далее мысленно двигаем целевую функцию вдоль вектора нормали внутри многоугольника. Последняя точка, которой коснется целевая функция в многоугольнике будет точка с координатой (2,0). Она получена пересечением целевой функции с прямой f₃.

Максимальное значение целевой функции мы найдем, подставив координаты точки (2,0) в уравнение целевой функции: f(X*)=4*2+2*0=8.

Значит, X*=(2,0) – оптимальный план и f(X*)=8 – максимальное значение целевой функции, что совпадает с ответом, полученным симплекс-методом.

3.Двойственная задача.

          Задача 1.                                                       Задача 2.

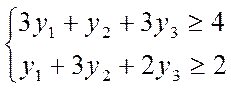
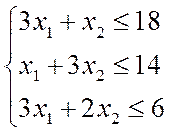
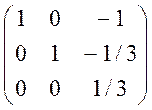Для того, чтобы X*=(2,0) был оптимальным планом задачи 1, необходимо и достаточно, чтобы существовал план Y*=(y₁*,y₂*,y₃*) двойственной ей задачи 2. Y* вычисляется по следующей формуле Y*=C*D^-1, значение которых находим из таблица 2: C*=(0,0,4), D*=

Получаем, что Y*=(0,0,4/3)-оптимальный план, а g(Y*)=18*0+14*0+6*4/3=8. Поэтому f(X*)=g(Y*)=8. Получили тот же результат.

21-40. Решить транспортную задачу. Заданы мощности поставщиков a_i, емкости потребителей b_j и матрица c_j стоимости перевозок единицы продукции от каждого поставщика каждому потребителю. Найти план перевозок, при котором суммарные транспортные затраты будут наименьшими.

Посчитаем суммарную мощность поставщиков и суммарную емкость потребителей: a₁+a₂+a₃=42 < b₁+b₂+b₃=60,  поэтому задача является открытой моделью транспортной задачи и для сведения ее к закрытой введем фиктивного поставщика с емкостью 60-42=18. Стоимости перевозки продукции от фиктивного поставщика к каждому потребителю положим равными нулю. В результате получим закрытую модель транспортной задачи:

Решим транспортную задачу с помощью метода потенциалов.

Составим исходный план перевозок X₁ методом «северо-западного угла».

Для плана X₁ число занятых клеток k=m+n-1=6, значит, план является невырожденным.

Суммарная стоимость перевозок по плану X_1:

f(X₁)=19*5+1*8+10*4+12*6=215.

Проверим план на оптимальность: найдем потенциалы u_i и v_j так, чтобы выполнялись условия 1⁰ и 2⁰ критериев оптимальности плана перевозок.

По условию 2⁰ для занятых клеток:

u₁+v₁=5       u₂+v₂=4        u₄+v₂=0

u₁+v₂=8       u₃+v₂=6        u₄+v₃=0

Зададим u₁=0, отсюда получим, что       u₂=-4, u₃=-2, u₄=-8, v₁=5, v₂=8, v₃=8.

По условию 1⁰ для свободных клеток:

Подставив потенциалы, получим:

0+8=8 > 3    -2+8=6 > 3   -2+5=3 < 7

-4+8=4 >2    -4+5=1 < 2  -8+5=-3 < 0

Мы видим, что не выполнено 3 неравенства из 6, причем,

.

Следовательно, план перевозок можно улучшить, введя перевозку

x₁₃= . С этой целью составим цикл, имеющий начало в клетке (1,3). В результате получим план