





ЛАБОРАТОРНАЯ РАБОТА № 78
ИЗУЧЕНИЕ СВОБОДНЫХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ В ЭЛЕКТРИЧЕСКОМ КОНТУРЕ
Цель работы: Исследовать зависимость напряжения на конденсаторе контура от времени при различных значениях активного сопротивления, рассчитать характеристики колебательного контура.
1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
|
Рис 1. Принципиальная схема реального колебательного контура |
Всякий реальный контур (состоящий из конденсатора С и катушки L) обладает активным сопротивлением R (рис. 1). Найдем уравнение колебаний в нем. Для этого условимся считать положительным ток, заряжающий конденсатор. Тогда
![]() .
(1)
.
(1)
Для цепи 1–R–L–2 запишем выражение закона Ома
JR = j1 – j2 + e12, где
j1 – j2 = –![]() –
напряжение на конденсаторе, e12 = es =
–
напряжение на конденсаторе, e12 = es = ![]() – ЭДС самоиндукции в катушке. Подставляя эти
выражения в закон Ома с учетом (1) получим однородное дифференциальное
уравнение второго порядка для заряда на левой обкладке (по схеме на рис. 1) конденсатора
– ЭДС самоиндукции в катушке. Подставляя эти
выражения в закон Ома с учетом (1) получим однородное дифференциальное
уравнение второго порядка для заряда на левой обкладке (по схеме на рис. 1) конденсатора
![]() . (2)
. (2)
Здесь
![]() – коэффициент
затухания;
– коэффициент
затухания; ![]() –
собственная частота колебаний в контуре (частота незатухающих колебаний в
соответствующем идеальном контуре). Простой подстановкой можно убедиться, что
общее решение уравнения (2) имеет вид (при условии, что b < w0)
–
собственная частота колебаний в контуре (частота незатухающих колебаний в
соответствующем идеальном контуре). Простой подстановкой можно убедиться, что
общее решение уравнения (2) имеет вид (при условии, что b < w0)
![]() , (3)
, (3)
где qm0 и a – постоянные интегрирования которые определяются из начальных условий. С учетом полученного для напряжения на конденсаторе U = j2 – j1 = q/C (с точностью до знака) имеем
![]() . (3a)
. (3a)
|
Рис. 2. График затухающих колебаний |
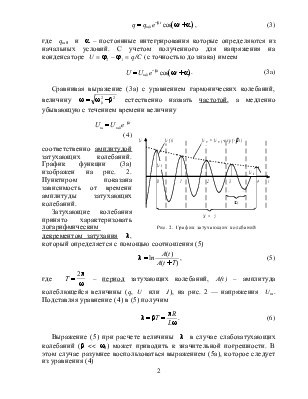
Сравнивая выражение (3а) с уравнением гармонических
колебаний, величину ![]() естественно назвать частотой, а медленно убывающую с течением
времени величину
естественно назвать частотой, а медленно убывающую с течением
времени величину
![]() (4)
(4)
соответственно амплитудой затухающих колебаний. График функции (3а) изображен на рис. 2. Пунктиром показана зависимость от времени амплитуды затухающих колебаний.
Затухающие колебания принято характеризовать логарифмическим декрементом затухания l, который определяется с помощью соотношения (5)
![]() , (5)
, (5)
где
![]() – период
затухающих колебаний, А(t) – амплитуда колеблющейся величины (q, U или J), на рис. 2 — напряжения Um. Подставляя уравнение (4) в (5) получим
– период
затухающих колебаний, А(t) – амплитуда колеблющейся величины (q, U или J), на рис. 2 — напряжения Um. Подставляя уравнение (4) в (5) получим
![]() . (6)
. (6)
Выражение (5) при расчете величины l в случае слабозатухающих колебаний (b << w0) может приводить к значительной погрешности. В этом случае разумнее воспользоваться выражением (5а), которое следует из уравнения (4)
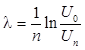 ,
(5а)
,
(5а)
т. е. использовать отношение амплитуд, разделенных целым числом периодов n (U0 – амплитуда в начальный момент времени; Un – амплитуда через интервал времени, равный n периодам). Из теории измерений следует, что формула (5а) дает минимальную погрешность в случае, когда для выдранных амплитуд приближенно выполняется условие U0/Un » 3 (в примере на рис. 2 n = 4).
Колебательный контур часто характеризуют его добротностью Q (практически используется только для слабозатухающих колебаний), которая определяется как отношение энергии, запасенной в контуре в данный момент времени, к средней потере энергии за время, в течение которого фаза колебаний изменяется на 1 радиан. Энергия, запасенная в контуре, пропорциональна квадрату амплитуды , тогда для ее потери за один период получаем
![]() .
.
С учетом того, что средняя потеря энергии за время изменения фазы на 1 радиан в 2p раз меньше, имеем
![]() , а
для слабозатухающих колебаний (2bT = 2l << 1) окончательно исходя
из определения добротности Q получим
, а
для слабозатухающих колебаний (2bT = 2l << 1) окончательно исходя
из определения добротности Q получим
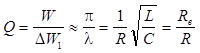 ,
(7)
,
(7)
где
величину 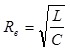 называют волновым сопротивлением контура.
называют волновым сопротивлением контура.
В случае, когда b ³ w0 вместо колебаний происходит апериодическое затухание. Этот режим часто используется, чтобы предотвратить нежелательные колебания различных систем (например в случае механических колебаний используют амортизаторы, заполненные маслом). Для электрических колебаний активное сопротивление контура, при котором колебательный процесс переходит в апериодический, называют критическим. Его значение можно найти из условия b = w0, откуда
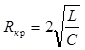 . (8)
. (8)
При практическом исследовании затухающих колебаний в контуре следует учитывать то, что любая реальная катушка индуктивности L имеет собственное активное сопротивление (R0), поэтому в выражениях для b, l и Q следует R заменить на сумму R + R0 , понимая под R теперь активное сопротивление внешнего резистора. В тех случаях, когда нельзя пренебречь величиной R0 по сравнению с R, для анализа затухающих колебаний удобно пользоваться соотношениями, получающимися из определений величин b, l и Q:
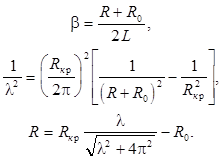 (9)
(9)
Практически во всех интересных случаях l << 2p, поэтому последнее из соотношений (9) переходит в
![]() . (9а)
. (9а)
В данной работе затухающие колебания в контуре из L, C и R возбуждаются посредством подачи на катушку через конденсатор малой емкости (С1) периодического напряжения прямоугольной формы со специального "калибрующего" выхода осциллографа. Сигналы, соответствующие крутым фронтам прямоугольников проходят через конденсатор, а в остальное время (в течение которого и наблюдаются затухающие колебания) его сопротивление для колебаний с частотой w достаточно велико (~ 105 Ом) и можно считать, что в это время соответствующий участок цепи разорван.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.