Министерство образования РФ
Санкт-Петербургский Государственный горный институт
им. Г.В.Плеханова
(технический университет)
Кафедра Механики
По дисциплине: Теория колебаний
Тема: Собственные колебания консервативной системы с одной степенью свободы вблизи положения устойчивого равновесия
Проверил: проф. Горшков Л.К.
2003
Система совершает малые
собственные колебания около положения равновесия. В задании приняты следующие
обозначения: 1- груз массы m1, прикрепленный
к точке А к свисающей с блока нити; 2- бицилиндр массы m2
с радиусами r и R и радиусом
инерции 
относительно его геометрической оси;
3- тонкий однородный стержень массы m3 и
длины l . Принять 
м/с2. Пружина имеет коэффициент жесткости с.
Найти уравнения движения груза при заданных начальных условиях, амплитуду, частоту и период его колебаний.
Дано:
m1=12кг
m2=24кг
m3=24кг
r2=3см
R2=8см
=4см
c=7200Н/м
l=150см
0,3см
1,2см/с
Решение:
Уравнение Лагранжа:
Кинетическая энергия системы:
T1+T2+T3=T
T1-энергия возвратно-поступательного движения груза 1
T2-энергия вращательного движения бицилиндра 2 вокруг неподвижной оси О
I2- момент инерции бицилиндра 2 относительно оси О;
угловая
скорость бицилиндра 2 относительно оси О;
Стержень 3 вращается вокруг О1. Значит
;
Для нахождения 
рассмотрим точки В и С, которые
движутся практически с одинаковыми скоростями:
;
;
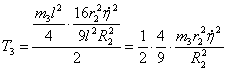
Потенциальная энергия системы.
П=П1+П2+Ппр
Мы рассматриваем малые колебания
системы. Поэтому угол 
мал и можно заменить синус
соответствующим углом. Таким образом:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
