данной конструкции предъявляется третья категория трещиностойкости.
Конструкция площадки приведена на рис 5.1
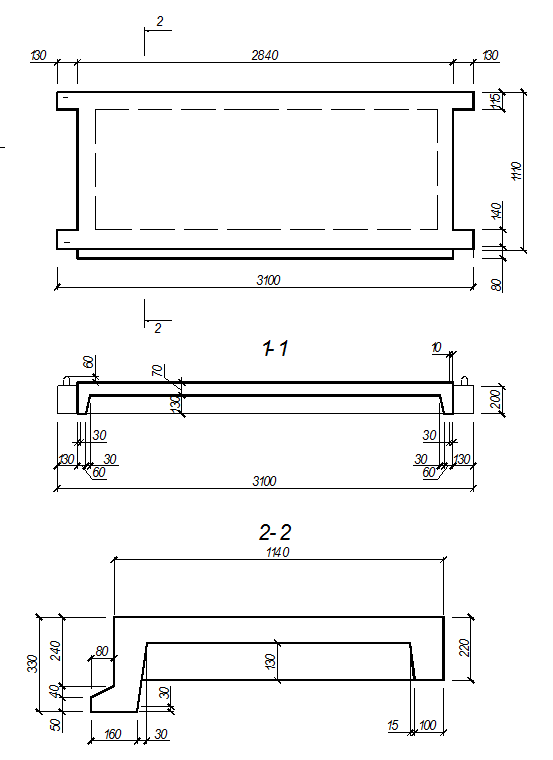
Рисунок 2.1- Конструктивные размеры площадки
2.2 Расчет плиты
Плита
опирается по периметру на контурные ребра. Отношение сторон плиты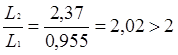 ;следовательно ее можно рассматривать как
балочную с пролетом в коротком направлении.
;следовательно ее можно рассматривать как
балочную с пролетом в коротком направлении. ![]() =0,955 м.
=0,955 м.
Подсчет нагрузки приведен в таблице 5.1
Таблица 2.1-Нагрузка на 1м2 плиты
|
Вид нагрузки |
Нормативная нагрузка, кН/м2 |
Коэффициент надежности, |
Расчетная нагрузка, кН/м2 |
ПостояннаяСобственная масса плиты с мозаичным слоем 25кН/м3∙0,09м |
2,25 |
1,1 |
2,48 |
|
Временная |
3,0 |
1,2 |
3,6 |
|
Полная |
|
|
Полку
плиты при отсутствии поперечных ребер рассчитывают как балочный элемент с
частичным защемлением на опорах.(рис 2.2). Расчетный пролет равен расстоянию
между ребрами ![]() =0,955
м.
=0,955
м.
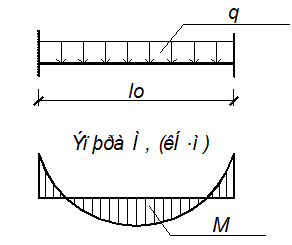
Рисунок 5.2- К определению расчетного пролета
При учете образования пластического шарнира изгибающий момент в пролете и на опоре находят по формуле 5.1, учитывающей выравнивание моментов
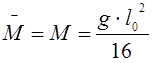 (2.1)
(2.1)
где ![]() =(
=(![]() +
+![]() )∙
)∙![]() =6,08 кН/м- расчетная нагрузка на 1м плиты;
=6,08 кН/м- расчетная нагрузка на 1м плиты;
![]() -расчетный
пролет.
-расчетный
пролет.
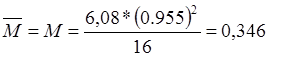 кН∙м;
кН∙м;
Рабочая высота сечения
![]() (2.2)
(2.2)
где ![]() -толщина полки;
-толщина полки;
![]() -расстояние от
растянутой грани до центра арматуры ;
-расстояние от
растянутой грани до центра арматуры ;
![]() см.
см.
При ![]() =100 см и
=100 см и ![]() см вычисляем:
см вычисляем:
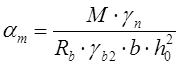 (2.3)
(2.3)
где М- расчетный изгибающий момент;
![]() - коэффициент надежности
,зависящий от класса ответственности здания
- коэффициент надежности
,зависящий от класса ответственности здания ![]() =0,95;
=0,95;
![]() -расчетное сопротивление
бетона сжатию;
-расчетное сопротивление
бетона сжатию;
![]() -коэффициент условия
работы бетона.
-коэффициент условия
работы бетона.
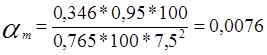 <αR
<αR
По табл. 2.12/ 2/определяем ζ и ξ ξ = 0,01; ζ = 0,995
По таблице 18 [2] ![]() 0,652>ξ
= 0,01, следовательно, сжатая арматура по расчету не требуется. Требуемая
площадь сечения рабочей арматуры:
0,652>ξ
= 0,01, следовательно, сжатая арматура по расчету не требуется. Требуемая
площадь сечения рабочей арматуры:
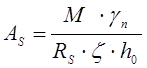 (2.4)
(2.4)
где ![]() 410 МПа=41кН/см2
расчетное сопротивление растяжению арматуры класса Вр-I .
410 МПа=41кН/см2
расчетное сопротивление растяжению арматуры класса Вр-I .
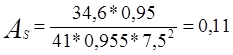 см2
см2
Принимаем сетку С-1 из арматуры диаметром 3 мм класса Вр-I с шагом S=200мм на 1 м длины с отгибом на опорах, Аs = 0,35 см2.
2.3 Расчет лобового ребра.
Расчетный
пролет ребра 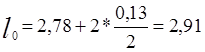
![]() м. В
работе участвует плита площадки как полка, расположенная в сжатой зоне.
м. В
работе участвует плита площадки как полка, расположенная в сжатой зоне.
Расчетное
сечение (рис.5.3) имеет следующие геометрические характеристики: ![]() = 32см,
= 32см, 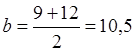 см;
см;![]() 18 см;
18 см; ![]() 7 см.
7 см.
При
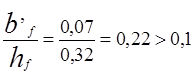 за расчетную ширину сжатой полки принимаем
из двух значений меньшее:
за расчетную ширину сжатой полки принимаем
из двух значений меньшее: ![]() см; и
см; и
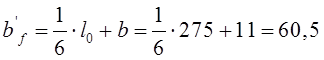 см. Принимаем
см. Принимаем ![]() 61 см.
61 см.
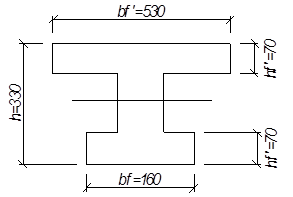
Рисунок 2.3 – К определению расчетного сечения
Подсчет нагрузки на 1 м ребра приведен в таблице 2.2.
Таблица 2.2- Нагрузка на 1м лобового ребра
|
Вид нагрузки |
Нормативная нагрузка, кН/м2 |
Коэффициент надежности, |
Расчетная нагрузка, кН/м2 |
ПостояннаяСобственная масса ребра (без учета свесов) (0,28м.0,095м+0,08м.0,05)∙1∙кН/м3 Собственная масса маршей (масса марша в кН) Временная нагрузка на маршах: Длительная
Кратковременная
|
0,765 10,2 1,44 2,88 |
1,1 1,1 1,2 1,2 |
0,842 11,2 1,73 3,46 |
|
Итого |
|
|
Таблица 2.2- Нагрузка на 1 м2 горизонтальной проекции
|
Вид нагрузки |
Нормативная нагрузка, кН/м2 |
Коэффициент надежности, |
Расчетная нагрузка, кН/м2 |
ПостояннаяСобственная масса плиты
Временная нагрузка на площадке: длительная
кратковременная |
1,18 0,65 1,3 |
1,1 1,2 1,2 |
1,3 0,78 1,56 |
|
Итого |
|
|
Расчетная схема лобового ребра показана на рисунке 2.4
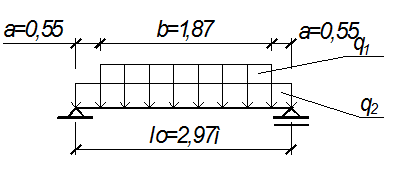
Рисунок 2.4- Расчетная схема лобового ребра
Усилия от полной расчетной нагрузки :
Изгибающий момент:
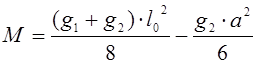 (2.5)
(2.5)
где ![]() -расчетная нагрузка на 1м лобового ребра включая
собственную массу ребра, маршей и временную нагрузку на маршах.
-расчетная нагрузка на 1м лобового ребра включая
собственную массу ребра, маршей и временную нагрузку на маршах.
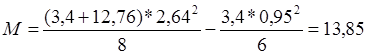 кН.м;
кН.м;
Поперечная сила:
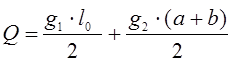 (2.6)
(2.6)
где ![]() 1,42 м- показано на рис
2.4;
1,42 м- показано на рис
2.4;
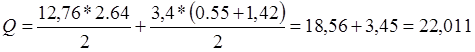 кН.
кН.
2.4 Расчет прочности нормальных сечений.
В соответствии с общим порядком расчета изгибаемых элементов определяем положение нейтральной оси по условию 5.7
![]() (2.7)
(2.7)
где ![]() - ширина полки расчетного таврового сечения;
- ширина полки расчетного таврового сечения;
![]() -толщина
полки таврового сечения;
-толщина
полки таврового сечения;
![]() -рабочая
высота сечения ;
-рабочая
высота сечения ; ![]() см.
см.
![]()
т.е условие соблюдается нейтральная линия проходит в
полке, поэтому сечение рассматриваем как прямоугольное шириной ![]() =53 см.
=53 см.
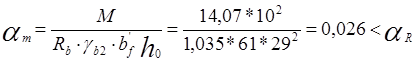
По табл. 2.12 /2/ определяем ζ и ξ ξ = 0,03; ζ = 0,985
По таблице 18 |2] ![]() >ξ
= 0,05 следовательно сжатая арматура по расчету не требуется.
>ξ
= 0,05 следовательно сжатая арматура по расчету не требуется.
Требуемая площадь сечения рабочей арматуры
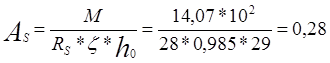 см2 ;
см2 ;
Принимаем два стержня диаметром 14 мм класса А-I с АS = 1,57 см2.
Процент армирования:
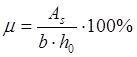 (2.8)
(2.8)
где ![]() -ширина ребра расчетного
таврового сечения;
-ширина ребра расчетного
таврового сечения;
![]() .
.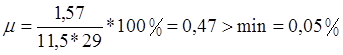
2.5 Расчет наклонного сечения лобового ребра на поперечную силу.
Поперечная сила на опоре Q=22,011кН. Вычисляем проекцию наклонного сечения на продольную ось c:
![]() (2.9)
(2.9)
где
![]() – коэффициент, учитывающий влияние вида
бетона;
– коэффициент, учитывающий влияние вида
бетона;
![]() – коэффициент, учитывающий влияние сжатых полок в
тавровых элементах;
– коэффициент, учитывающий влияние сжатых полок в
тавровых элементах;
![]() – коэффициент, учитывающий влияние продольных сил;
– коэффициент, учитывающий влияние продольных сил;
![]() =0.
=0.
![]() -расчетное сопротивление бетона растяжению;
-расчетное сопротивление бетона растяжению;
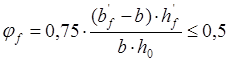 (2.10)
(2.10)
где
![]() см;
см;
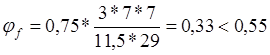 ;
;
![]() =1+0,33+0=1,33<1,5;
=1+0,33+0=1,33<1,5;
![]()
В расчетном наклонном сечении поперечное усилие воспринимается бетоном:
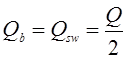 (2.11)
(2.11)
тогда
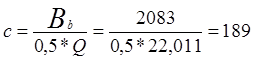 см, что больше
см, что больше ![]() =2∙29см=58см,
принимаем с=60см.
=2∙29см=58см,
принимаем с=60см.
Вычисляем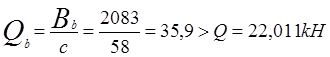 .
.
Следовательно, поперечная арматура по расчету не требуется. По конструктивным требованиям принимаем закрытые хомуты (учитывая изгибающий момент на консольном выступе) из арматуры диаметром 6 мм класса A-I шагом 150 мм.
Консольный выступ для опирания сборного марша армируем сеткой С-2 из арматуры диаметром 6 мм класса A-I, поперечные стержни этой сетки скрепляют с хомутами каркаса Кр-1 ребра.
2.6 Расчет пристенного продольного ребра.
Подсчет нагрузки на 1 м ребра приведен в таблице 2.4
Таблица 2.4- Нагрузка на 1м пристенного продольного ребра
|
Вид нагрузки |
Нормативная нагрузка, кН/м2 |
Коэффициент надежности, |
Расчетная нагрузка, кН/м2 |
ПостояннаяСобственная масса ребра 0,115м.0,13м∙25кН/м3 Собственная масса плиты (0,09м∙0,885м∙25кН/м3)/2 Временная :
|
0,373 1,76 1,695 |
1,1 1,1 1,2 |
0,410 1,294 2,034 |
|
Итого |
|
|
Расчетная схема пристенного ребра такая же, как и лобового ребра.
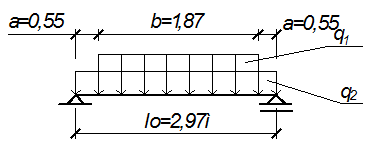
Рисунок 2.4-Расчетная схема пристенного ребра
Форму
сечения условно принимаем тавровую с размерами: ![]() 10,15см,
10,15см,
![]() 22 см;
22 см;
![]() ;
; ![]() 0,07м.
0,07м.
Изгибающий момент:
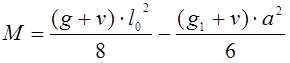 (2.12)
(2.12)
где ![]() - полная расчетная нагрузка на 1м ребра;
- полная расчетная нагрузка на 1м ребра;
![]() - расчетная
нагрузка на 1м без учета свеса ребра;
- расчетная
нагрузка на 1м без учета свеса ребра;
![]() -расчетный
пролет ребра .
-расчетный
пролет ребра .
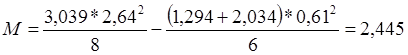 кН.м;
кН.м;
Поперечная сила:
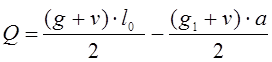 (2.13)
(2.13)
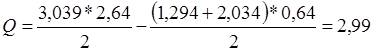 кН.
кН.
Рабочая высота сечения ; ![]() см.
см.
Определяем случай расчета таврового сечения:
![]() (2.14)
(2.14)
где ![]() - ширина полки расчетного таврового сечения;
- ширина полки расчетного таврового сечения;
![]() -толщина
полки таврового сечения;
-толщина
полки таврового сечения;
![]() -рабочая высота сечения ;
-рабочая высота сечения ;
![]()
т.е
условие соблюдается нейтральная линия проходит в полке, поэтому сечение
рассматриваем как прямоугольное шириной ![]() =0,638 м.
=0,638 м.
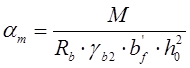 (2.15)
(2.15)
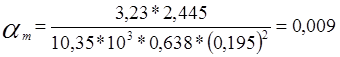
По табл. 2.12 /2/ определяем ζ и ξ ξ = 0,01; ζ = 0,995.
Требуемая площадь сечения рабочей арматуры по формуле 5.4
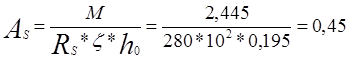 см2
;
см2
;
Принимаем два стержня диаметром 10 мм класса А-I с АS =1,57 см2.
Поперечная сила Q=2,99 кН.
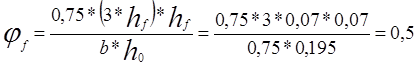 ;
;
Принимаем ![]() ∙
∙![]() =1+0,58 +0=1,58;
=1+0,58 +0=1,58;
По формуле2.9 определяем :
![]() ;
;
Величина проекции наклонного сечения с на продольную ось:
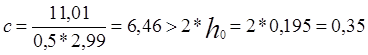 м, что больше
м, что больше ![]() =2∙17,5см=35см,
принимаем с=39см.
=2∙17,5см=35см,
принимаем с=39см.
Вычисляем
поперечное усилие воспринимаемое бетоном 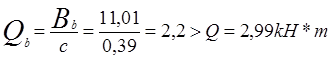 .
.
Следовательно, поперечная арматура по расчету не требуется. По конструктивным требованиям принимаем поперечные стержни диаметром 3 мм класса A-I .
Шаг
поперечных стержней на приопорных участках ![]()
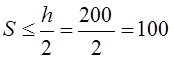 мм. На среднем участке
мм. На среднем участке 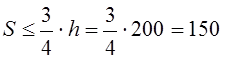 мм.
мм.
5.7 Расчет поперечных ребер.
Поперечные ребра армируем конструктивно; продольные стержни принимаем диаметром 8 мм класса A-I, поперечные диаметром 6 мм класса A-I через 100 мм на крайних участках и через 200 мм на среднем участке
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.