Расчет балконной плиты. Характеристики прочности бетона и арматуры. Расчет ригеля поперечной рамы. Расчет колонны

Максимальная поперечная сила на опоре от расчетной нагрузки:

Vsd=q*l*gn/2                                                                                                (4.8)

Vsd=14.66*5.85*0.95/2=40.74kH

Vrd.ct,min=57.37 kH больше Vsd=40,74 kH

Следовательно, по расчету поперечная арматура не требуется.

4.1.5. Проверка панели на монтажные нагрузки.

Панель имеет четыре монтажные петли из стали S400, расположенные на расстоянии 35 см от концов панели. С учетом коэффициента динамичности Kd=1.4 расчетная нагрузка от веса панели:

q=Kd*gf*g*b                                                                                                  (4.9)

где  g-собственный вес панели:  g=hred*S

b-конструктивная ширина панели

gf-плотность бетона

S-приведенная толщина панели

hred=0,185/1,5=0,12м

q=0,12*2500=3000Н/м2

q=1,4*1,1*3000*1,5=6930Н/м

Отрицательный изгибающий момент консольной части панели:

М=q*h²/2=6930*0.35²/2=424.5Н*м

Этот консольный момент воспринимается продольной монтажной арматурой каркасов. Полагая, что z1=0.9d. требуемая площадь сечения указанной арматуры составляет:

As=M/z1*fyd                                                                                                    (4.10)

As=42450/0.9*19*365*100=0.068см²

 

При подъеме панели вес ее может быть передан на две петли. Тогда усилие на одну петлю составляет:

N=q*l/2=6930*6/2=20790H

As=N/fyd=20790/365*100=0.57см2

Принимаем конструктивно арматуру S400 диаметром12;As=

1.1  Характеристики прочности бетона и арматуры.

Бетон тяжелый класса В25:

R_bn=R_b.ser=18.5 МПа, R_b=14.5 МПа;  γ_b2=0.9;  R_bth=R_bt.ser=1.6 МПа; 

R_bt=1.05 МПа;  E_b=30000 МПа.

Арматура класса А400:

R_sn=390 МПа; R_s=365 МПа; E_s=200000 МПа.

1.2  Расчет прочности плиты по сечению, нормальному к продольной       оси.

М=119.42  кН*м.

Расчет производим согласно п. 3.22 [1] в предположении, что сжатая арматура по расчету не требуется.

Проверяем условие 32 [1], принимая А’_s=0

Для этого вычисляем:

R_b*b’_f*h’_f*(h_o-0.5* h’_f)=14.5*1.97*0.03*(0.17-0.5*0.03)*10³=132.83 кН*м>M=119.42 кН*м, то есть граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной b= b’_f=1.97м.

Вычислим значение:

α_m=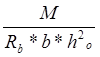==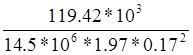0.145< α_R=0.422

α_R=0.422

определено по таблице 18[1].

То есть сжатая арматура действительно не требуется по расчету.

Площадь сечения растянутой арматуры вычислим по формуле 23 [1]. Для этого по таблице 20 [1] при α_m=0.145 находим ζ=0.925, тогда

А_s=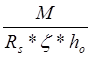=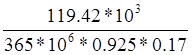*10⁶=2080 мм²

Далее по приложению 4 [1] принимаем 5Æ25 А400 с общей площадью А_s=2454 мм²

1.3  Расчет прочности плиты по сечению, наклонному к продольной оси.

(Q=82.4 кН)

Для начала определяем необходимость установки поперечной арматуры. Для этого проверяем выполнение следующих условий:

Q_max≤2.5*R_bt*b*h_o; условие 71[1]

Q≤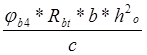; условие 72[1]

Проверяем выполнение условия 71 [1]:

Q_max=82.4≤1.05*10³*1.97*0.17=351.7 кН

Проверяем выполнение условия 72 [1]:

Q=82.4≤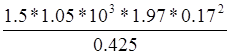=210.98 кН

Оба условия выполняются, следовательно поперечная арматура по расчету не требуется.

Поперечную арматуру устанавливаем конструктивно. По приложению 9[1],исходя из соотношения диаметров свариваемых стержней принимаем поперечную арматуру диаметром 8 мм с шагом 150 мм.

1.7  Расчет многопустотной плиты по предельным состояниям второй группы.

1.7.1 Расчет многопустотной плиты по образованию трещин нормальных к продольной оси элемента.

Для определения необходимости расчета по образованию трещин находим:

µ=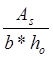==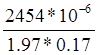0.007

Так как µ=0.007>0.005 согласно требованиям п. 4.1[1] принимаем без расчета, что рассматриваемый элемент имеет трещины нормальные к продольной оси на наиболее напряженных участках.

1.7.2 Расчет многопустотной плиты по раскрытию трещин нормальных к продольной оси элемента.

Ширину раскрытия трещин, нормальных к продольной оси элемента, a_crc, мм, следует определять по формуле:

a_crc=δ*φ_l*η**20(3.5-100µ₁)*, где δ- коэффициент, принимаемый равным для изгибаемых элементов 1.0,

φ_l- коэффициент, принимаемый равным при учете продолжительного действия постоянных и длительных нагрузок для конструкций из тяжелого бетона:

φ_l=1.60-15µ_1,

φ_l=1.60-15*0.007=1.495_,

η- коэффициент принимаемый равным для арматуры класса А400 – 1.0,

µ₁- коэффициент армирования сечения, принимаемый равным:

µ₁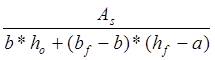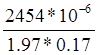₌==0.007

d- диаметр растянутой арматуры, d=25 мм,

σ_s- напряжение в стержнях крайнего ряда арматуры, определяемое по формуле 259 [1]:

σ_s=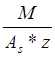, где z- расстояние от центра тяжести растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной, определяемое по формуле:

z=h_o*,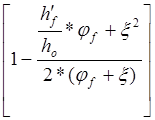

z=0.17*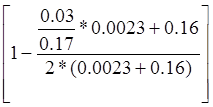=0.086м=86мм, где φ_f=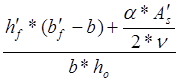==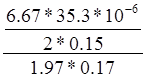0.0023

Тогда:

σ_s=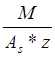=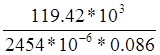*10^-6=567.48 Mpa,

Тогда:

a_crc=δ*φ_l*η**20(3.5-100µ₁)*=1*1.495*1*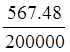*20(3.5-100*0.007)*=0.2мм, что меньше предельно допустимой величины [a_crc]=0.3мм.

1.7.3 Расчет многопустотной плиты по образованию трещин наклонных к продольной оси элемента.

Согласно п. 4.4 [1] участки по длине элемента, на которых отсутствуют наклонные трещины, определяется из условия (248):

Q≤φ_b3*R_bt,ser*b*h_o

φ_b3- определяется по таблице 21 [1], в нашем случае φ_b3=0.6

Тогда условие (248) примет вид:

Q=82.4≤1.6*10³*1.97*0.17=535.84 кН,

Условие выполняется, следовательно наклонные трещины, по длине элемента отсутствуют.

1.7.4   Расчет прогиба плиты.

Для изгибаемых элементов при >10,=29>10, прогиб, согласно п. 4.29 [1] определяется по формуле 311 [1]:

f=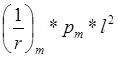, где - кривизна элемента определяемая по формуле (309) [1],

p_m- коэффициент принимаемый по таблице 35 [1],

Определяем кривизну:

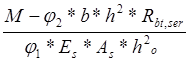=, где φ₁ и φ₂- коэффициенты принимаемые по таблице34 [1]. В нашем случае φ₁ и φ₂ соответственно равны 0.4 и 0.53.

Тогда кривизна:

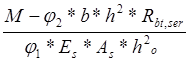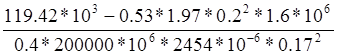===0.0083,

p_m-

Тогда прогиб:

f=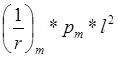=0.0083**5.8²=0.029м=29мм, что меньше предельно допустимого значения определяемого по таблице2 [1] и равного 0,03м=30 мм.

2.  РАСЧЕТ РИГЕЛЯ ПОПЕРЕЧНОЙ РАМЫ.

2.1 Определение усилий в ригеле поперечной рамы.

2.1.1   Нагрузки.

Вычисляем расчетную нагрузку на 1м длины ригеля.

Постоянная: от перекрытия с учетом коэффициента надежности по назначению здания 4.134*5.9*0.95=23.17 кН/м от веса ригеля сечением 0,2х0,45м с учетом коэффициентов надежности