Расчет статически неопределимой системы в условиях работы составляющих ее элементов в режиме растяжения – сжатия

Министерство образования Российской Федерации

Санкт–Петербургский государственный горный институт им. Г.В.Плеханова

(технический университет)

Кафедра механики

Расчетно – графическое задание

 Вариант №7

Сопротивление материалов

По дисциплине  ____________________________________________________________________________

^{(наименование учебной дисциплины согласно учебному плану)}

Автор: студент группы ТПП-01-2   ___________   / Кириллов К.В. /

Оценка:   ___________

Дата:   ___________

Проверил:   ___________

Руководитель работы:   ___________   / Зорецкий. /

Санкт-Петербург

2003

Целью данного задания является расчет статически неопределимой системы в условиях работы составляющих  ее элементов в режиме растяжения – сжатия. Рассчитываемая система представляет собой стержневую конструкцию с одной шарнирной опорой и двумя деформируемыми тягами.                                                   

Заданы материалы стержней: 1-алюминий, 2-сталь,  упругие модули на растяжение (сжатие):Е₁ = 0,7·10⁵ мПа, Е₂ = 2·10⁵ мПа,  внешние силы Р₁ = 5·10⁴ Н, Р₂ = 3·10⁴ Н,  коэффициенты линейного расширения  материалов стержней  = 26·10^{-6  0}С^-1,   = 12·10^{-6  0}С^-1.

Неточность изготовления элемента системы: стержень 1 изготовлен короче на величину  d = -0,0002 l₁. Изменение температуры системы: стержень 1 -Т = 30  ⁰С; стержень 2 - Т = 0  ⁰С. Допустимые напряжения для материалов каждого из стержней: ₁ = 60 мПа, ₂ =160 мПа.  Конструктивное соотношение площадей стержней: F₂/F₁ = 1. Геометрические размеры: a =1,5м  ,  b = 0,8м  , c = 0.5м  , d = 0,4м  , h = 1м , a₁ =60⁰ ,   a₂ = 45⁰.

Определить величины F₁, F₂; учитывая, что балка AD предполагается абсолютно  жесткой невесомой.                

                                                                                                                      

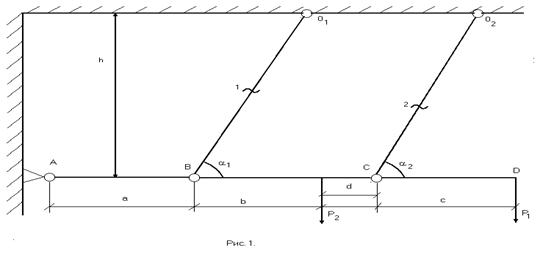
1.Определение усилий от внешней силы P (Т=0; d=0)

M_A = -N₁× a × sin a_{1 +} P₂ (a+b) - N₂ (a+b+d) × sin a₂ – P₁ (a+b+d+c)=0

или

N₁× a × sin a₁  + N₂ (a+b+d) × sin a₂ =P₂ (a+b) + P₁ (a+b+d+c)             (1)

Для составления одного уравнения совместности деформаций необходимо рассмотреть схему перемещений системы (рис.3)

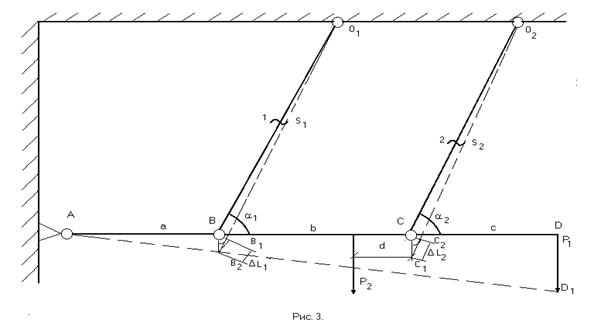
Под действием сил P₁ и P ₂ первый стержень удлинится на величину  l₁, второй  на l₂. Балка AD₁. Ввиду малости упругих деформаций горизонтальными смещениями точек В и С, лежащих на оси балки, пренебрежем и будем считать, что точки В и С в ходе деформации системы переместятся строго вертикально и займут положение В₁ и С₁.