Отрезки В1
В2 и С1 С2 определяют удлинение
соответственно ![]() l1
и
l1
и ![]() l2.
l2.
Треугольник АВВ1подобен треугольнику АСС1
![]() =
= ![]() ;
(2)
;
(2)
Из треугольника ВВ1В2 и треугольника СС1С2 определяем:
BB1 = ![]() ; CC1
=
; CC1
= ![]() ;
(3)
;
(3)
Подставим (3) в(2) получим уравнение совместности деформации заданной стержневой системы
![]() l1=
l1=![]() l2×
l2×![]()
![]() (4)
(4)
или ![]() l1 =
l1 =![]() l2 × K, где К=
l2 × K, где К=![]()
Используя закон Гука для каждого из стержней:
![]() l1 =
l1 =![]() ;
; ![]() l2 =
l2 = ![]()
Из уравнения (4) получим:
![]() =
= ![]() ×
× ![]()
![]() (5)
(5)
Учитывая, что l1=![]() ; l2=
; l2=![]() перепишем (5) в виде
перепишем (5) в виде
![]() (6)
(6)
Решая совместно систему уравнений (1)и (6) получаем
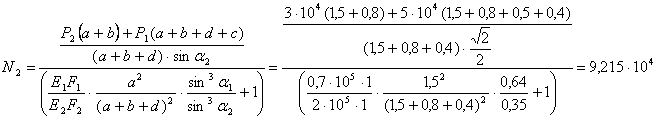
 Из выражения (7)при отношении
Из выражения (7)при отношении ![]() =1
находим:
=1
находим:
N1 = 2,691 × 104 Н (растяжение)
N2 = 9,215 × 104 Н (растяжение)
Проверка правильности найденных численных значений производится путем подстановки N1 и N2 в уравнение равновесия:
N1× a × sin a1 + N2 (a+b+d) × sin a2 =P2 (a+b) + P1 (a+b+d+c)
2.691×104× 1.5 ×![]() +9.215×104×2.7×
+9.215×104×2.7×![]()
2.Определение
напряжений вызванных неточностью изготовления стержней (P=0; ![]() T=0; d¹0)
T=0; d¹0)
Пусть первый
стержень изготовлен короче по длине - d1.
При сборке в них появятся внутренние напряжения. Расчетная схема
представлена на (рисунке 4).Знаки внутренних усилий будут разными, т.к. при
сборке необходимо первый стержень растянуть на величину![]() l1,
и в нем появятся растягивающие усилия N1. Второй
стержень будет сопротивляться этому, что приведет к необходимости его сжатия на
величину
l1,
и в нем появятся растягивающие усилия N1. Второй
стержень будет сопротивляться этому, что приведет к необходимости его сжатия на
величину ![]() l2;
и в нем возникнут сжимающие усилия N2.
l2;
и в нем возникнут сжимающие усилия N2. 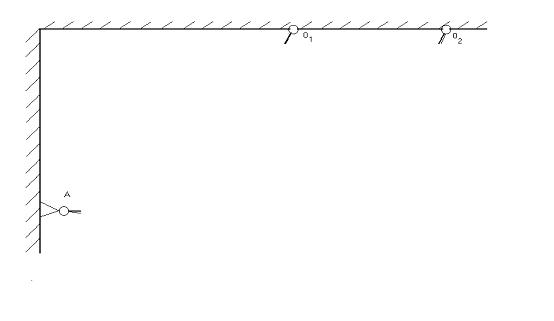
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.