Определение дисперсии при заданном математическом ожидании. Рассчет параметров сигнала и шума

Предварительное задание к лабораторной работе №1

Задание:

1. Определить дисперсию s2 при заданном математическом ожидании m = 1, если =+, где  - номер бригады, а  - последняя цифра в номере группы.

2. Рассчитать длину реализации , при которой относительная ошибка %. Округлив значение  до ближайшего кратного  (т. к. при моделировании случайных процессов длина реализации устанавливается кратной 1024), найти соответствующее ему значение

Дано:

Решение:

1. Определение дисперсии

дисперсия

2.

Относительная ошибка:     =      отсюда:     =

Т. к.  = , тогда  =  =

Округляем до  

Тогда соответствующее ему значение:

 =  =  или 3%

Предварительное задание к лабораторной работе №2

Задание:

1. Рассчитайте параметры сигнала и шума, при которых полученное на выходе СФ ОСШ  = 6.2 - 0.2(+), где  -номер бригады;  - последняя цифра в номере группы. Длительность сигнала рекамендуется выбирать в пределах 0.1...0.2*(1024*Dt), где Dt - интервал дискретизации.

2. Рассчитайте  зависимость ОСШ на выходе квазиоптимальных фильтров от постоянной времени интегрирующего звена первого порядка. Найдите оптимальные значения, параметров, обеспечивающих максимальное ОСШ, и проигрыш по сравнению с СФ.

3. Рассчитайте длинну реализации , при которой относительная ошибка измерения дисперсии шума на выходе СФ не превышает 3%.

Дано:

- относительная ошибка измерения

Решение:

1.

ОСШ на выходе СФ:

с  - интервал дискретизации

с  - длительность сигнала

Сигнал - видеоимпульс с амплитудой U=1 В и длительностью

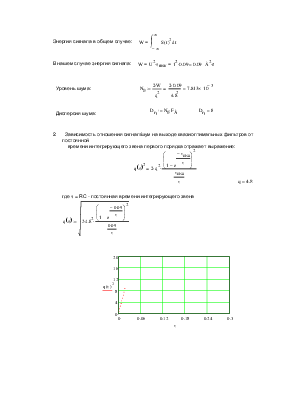
Энергия сигнала в общем случае:     =  

В нашем случае энергия сигнала:     =  =  

Уровень шума:                                   =

Дисперсия шума:

2.

Зависимость отношения сигнал/шум на выходе квазиоптимальных фильтров от постоянной времени интегрирующего звена первого порядка отражает выражение:

 =   

где t = RC - постоянная времени интегрирующего звена

Из графика видно, что максимальное значение ОСШ достигается при постоянной времени интегрирующего звена   =  = 0.06 =  .

В этом случае значение ОСШ будет соответствовать:    =    =

Проигрыш =  =  или  10.3%

3.

Относительная ошибка измерения дисперсии шума на выходе СФ описывается выражением:    e =      отсюда:     =  =

Округления оптимальной длины реализации до 1024 не требуется.

Если учитывать тот факт, что до прохождения фильтра, соседние отсчеты шума были некоррелированными, т.е. при вычислении , можно было принять   =  =  , где принималось F = 1024, а  =  .

 - Интервал дискретизации:            

То в данном случае, т.е. после прохождения согласованного фильтра, число отсчетов уменьшилось и необходимо принять  =  =  с, тогда окончательно:

 =  =

Округляем, и получаем длину реализации, при которой относительная ошибка измерения дисперсии шума на выходе СФ не превышает 3%:  

 = 400