Новосибирский Государственный Технический Университет
Кафедра
Теоретических основ радиотехники
Измерение характеристик случайных процессов
Факультет: РЭФ
Группа: РТ5-03
Студенты: Панарин А.С.
Преподаватель:
Новосибирск
2003
Цель работы. Изучение методов измерение характеристик некоторых случайных процессов.
Вариант 1. Измерение средней величины
1.
Включите генератор Гауссовского
случайного процесса с прямоугольной спектральной плотностью мощности. Установите
математическое ожидание и дисперсию, при которых 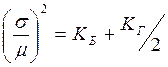 , где KБ – номер
бригады в лабораторном журнале, а KГ – последняя цифра в номере группы. Наблюдайте осциллограммы.
Исходные данные:
, где KБ – номер
бригады в лабораторном журнале, а KГ – последняя цифра в номере группы. Наблюдайте осциллограммы.
Исходные данные:
KБ = , KГ = 3, σ = μ =
2.
Рассчитайте длину реализации KS,
при которой относительная ошибка составляет ![]() .
Округлив значение KS до ближайшего кратного K = 1024 (При длине
моделирования случайных процессов длина реализации устанавливается кратным
1024), найдите соответствующее ему значение
.
Округлив значение KS до ближайшего кратного K = 1024 (При длине
моделирования случайных процессов длина реализации устанавливается кратным
1024), найдите соответствующее ему значение ![]() .
Измерьте значение μ при найденном KS.
.
Измерьте значение μ при найденном KS.
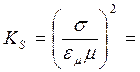
Округляем найденное значение дол ближайшего кратного
1024, и находим соответствующее ему значение ![]() .
. ![]() =
=
KS =
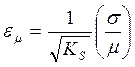 =
=
3.
Проведите качественный анализ
оценки ![]()
-
убедитесь в несмещенности ![]() ;
;
-
убедитесь в состоятельности ![]() ;
;
4. Экспериментально определите дисперсию оценки; убедитесь в ее соответствии теоретическому значению.
5.
Увеличьте среднеквадратичное
значение σ процесса x(t) вдвое;
измерьте значение μ при неизменных значениях всех остальных параметров
случайного процесса. Оцените экспериментально относительную погрешность.
Предложите и реализуйте метод снижения относительной ошибки ![]() до прежнего значения, подтвердив
экспериментально достижение этого результата.
до прежнего значения, подтвердив
экспериментально достижение этого результата.
6.
Профильтруйте случайный процесс в
фильтре нижних частот с прямоугольной АЧХ, полоса пропускания которого в 10 раз
уже спектра исходного процесса. Установите энергетические параметры σ и μ,
так, чтобы и в п. 1 обеспечивалось требование 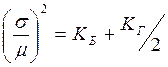 . Значение шага дискретизации должно остаться прежним.
Проведите эксперимент, определяющий качество оценки μ в этих условиях. Как
можно восстановить прежнее качество оценки?
. Значение шага дискретизации должно остаться прежним.
Проведите эксперимент, определяющий качество оценки μ в этих условиях. Как
можно восстановить прежнее качество оценки?
7. Предложите метод измерения среднего значения, при котором вместо алгоритма (1), (2) используется фильтр. Проведите эксперимент подтверждающий работоспособность предложенного решения.
Вариант. 2 ИЗМЕРЕНИЕ СРЕДНЕГО ЗНАЧЕНИЯ
Выполните
пп1…8 лабораторного задания варианта 1 для гауссовского случайного процесса с
корреляционной функцией вида ![]() . ПРИ выполнении пункта
6., в отличие от п.6 варианта 1, применить фильтр с импульсной характеристикой
вида
. ПРИ выполнении пункта
6., в отличие от п.6 варианта 1, применить фильтр с импульсной характеристикой
вида ![]() .
.
Вариант 3. ИЗМЕРЕНИЕ ДИСПЕРСИИ
1.
Включите генератор Гауссовского
случайного процесса с прямоугольной спектральной плотностью мощности.
Установите математическое ожидание и дисперсию, при которых 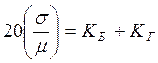 , где KБ – номер
бригады в лабораторном журнале, а KГ – последняя цифра в номере группы.
, где KБ – номер
бригады в лабораторном журнале, а KГ – последняя цифра в номере группы.
2.
Рассчитайте длину реализации KS,
при которой относительная ошибка составляет ![]() .
Округлив значение KS до ближайшего кратного K = 1024 (При длине
моделирования случайных процессов длина реализации устанавливается кратным
1024), найдите соответствующее ему значение
.
Округлив значение KS до ближайшего кратного K = 1024 (При длине
моделирования случайных процессов длина реализации устанавливается кратным
1024), найдите соответствующее ему значение ![]() .
Измерьте значение σ2 при найденном KS.
.
Измерьте значение σ2 при найденном KS.
3. Проведите качественный анализ оценки сто бы убедится в ее состоятельности.
4. Экспериментально определите дисперсию оценки; убедитесь в ее соответствии теоретическому значению. При μ = 0, μ, установленное согласно пункту 1.
5. Увеличьте среднеквадратичное значение σ процесса x(t) вдвое;
Оцените экспериментально:
- абсолютную погрешность
- относительную погрешность
Сопоставьте с результатами п.4
6. Профильтруйте случайный процесс в фильтре нижних частот с прямоугольной АЧХ, полоса пропускания которого в 10 раз уже спектра исходного процесса. Установите энергетические параметры σ и μ, так, как и в п. 1. Значение шага дискретизации должно остаться прежним. Проведите эксперимент, определяющий качество оценки μ в этих условиях. Как можно восстановить прежнее качество оценки?
7. Предложите метод измерения σ2. Докажите работоспособность метода.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.