Измерение характеристик случайных процессов. Измерение дисперсии

Министерство образования и науки Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра ТОР

Лабораторная работа №1

Измерение характеристик случайных процессов

Вариант 3. Измерение дисперсии.

Факультет РЭФ

Группа: РТ5-02

Студент: Шелковникова Н.М.

Преподаватель: Мархакшинов А.Л.

2013

Цель работы: Изучение методов измерения некоторых характеристик случайных процессов.

В данной работе изучаются методы, используемые при измерении основных вероятностных характеристик непрерывных случайных процессов (СП).

В работе рассматриваются эргодические случайные процессы, для измерения характеристик которых можно применять усреднение по времени в пределах одной реализации вместо значительно более сложного усреднения по ансамблю, используемого при отсутствии эргодического свойства. Изучается измерение моментов - математического ожидания и дисперсии, а также вероятности превышения порога.

Ход работы:

1) Включим генератор гауссовского СП с прямоугольной спектральной плотностью мощности. Установим математическое ожидание  и дисперсию ,при которых 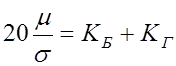,                                                               (1)

где  = 4,

 = 2.

Из формулы (1) необходимо выразить , и затем посчитать это значение:

Во вкладке генератор выбираем:           

Шум с равномерной спектральной плотностью мощности - генератор случайного процесса с равномерной в полосе частот  спектральной плотностью мощности.

Управляемые параметры : а) математическое ожидание;

б) дисперсия.

Устанавливаем полученное значение дисперсии.

2) Рассчитаем длину реализации , при которой относительная ошибка

.

Рассчитываем по формуле:

Округляем значение  до ближайшего кратного  (при моделировании случайных процессов длина реализации устанавливается кратной 1024).

20 блоков по 1024 повторений = 20480

Находим соответствующее значение   .

Измерим значение  при найденном :

_тек = 10,75685

_сумм = 11,051865

3) Проведем экспериментально качественный анализ оценки с целью убеждения ее состоятельности.

_сумм =

Второй столбец значений рассчитаем по формуле: где n – значения от 1до 20,

 - рассчитанная дисперсия, равна 11,2.

Получаем значения:

D(n)    =

По полученным значениям строим график (Рис.1.1):

Рис.1.1.  Качественный анализ оценки реализации.

4) Экспериментально определим дисперсию оценки   при  и , установленном согласно п.1. Сопоставим экспериментальные и теоретические результаты.

Для этого берем 15 оценок:

_сумм  =

_сумм -  =

Полученные значения возводим в квадрат:

(_сумм - )²  =

Суммируем:

= 0.255

Делим на общее количество оценок:

0,255/15=0,017

Получено экспериментальное значение оценки, 1,7 %. Теоретическое значение 1 %.

5) Увеличим вдвое значение  и проведем заново измерения. Оценим экспериментально:

·  абсолютную погрешность;

·  относительную погрешность.

Сопоставим результаты с п.4.

=11,1

Увеличим вдвое значение :

(2·)² = 4·11,1=44,4

Далее оцениваем относительную погрешность:

Для этого берем 10 оценок:

_сумм  =

Из полученных значений вычитаем новое значение дисперсии, =44,4:

_сумм -  =

Возводим в квадрат:

(_сумм - )²  =

Полученные значения суммируем:

= 3,625

Делим на общее количество оценок:

3,625/10=0,3625

Извлекаем из данного значения корень:

=0,602

Делим на удвоенное значение дисперсии:

0,602/44,4=0,014

Полученное значение относительной погрешности: 1,4% получилось меньше, чем в п.4: 1,7%. Теоретическое значение погрешности: 1%.

6)  Профильтруем СП в фильтре с прямоугольной АЧХ, полоса пропускания которого в 10 раз уже исходного процесса, и, сделав предварительные расчеты, установим у профильтрованного СП прежние значения  и . Проведем эксперименты, определяющие качество оценки  в этих условиях.

Верхняя частота: 1024 Гц.

_сумм =

Второй столбец значений рассчитаем по формуле: где n – значения от 1до 20,

 - рассчитанная дисперсия, равна 11,2.

Получаем значения:

D(n)    =

По полученным значениям строим график (Рис.1.2):

Рис.1.2.  Качественный анализ оценки реализации.

Сопоставим график полученный в п.3 с графиком полученным в п.6.

Рис.1.3.  Совмещенные графики из п.3 и п.6.

Рис.1.4.  Совмещенные графики из п.3 и п.6.

Вывод:  Изучены методы измерения некоторых характеристик случайных процессов, в данном варианте это была – дисперсия.

В данной работе изучались методы, используемые при измерении основных вероятностных характеристик непрерывных случайных процессов (СП). Изучение проводилось при помощи цифровых моделей сигналов и измерителей. Такой способ имеет много достоинств, некоторые из них: гибкость такого подхода, сравнительная простота имитации многих метрологических задач, цифровые измерители имеют и чисто практическое значение. Это находится в общем русле развития измерительной техники, одна из тенденций которого заключается во все более широком применении цифровых методов и средств.