Математические модели сигнала. Представление сигнала в базисе Функций Уолша

Министерство образования  и науки Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

_____________________________________________________________________

Кафедра теоретических основ радиотехники (ТОР)

                    РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ

                                               ЗАДАНИЕ N 1

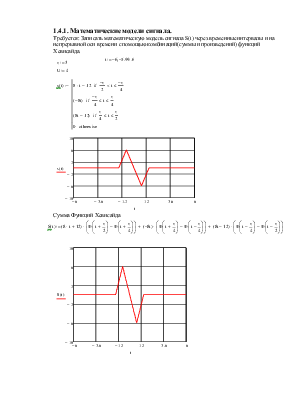
1.4.1. Математические модели сигнала.

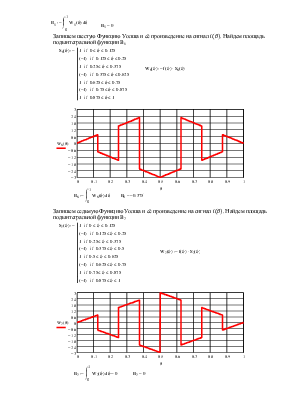
Требуется: Записать математическую модель сигнала S(t) через временные интервалы и на непрерывной оси времени с помощью комбинаций(суммы и произведений) функций Хевисайда.

Сумма Функций Хевисайда

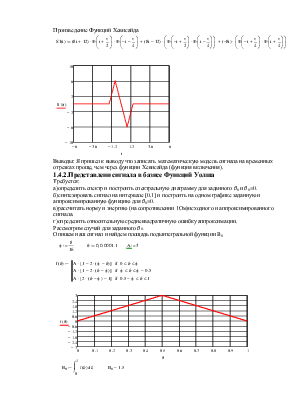
Произведение Функций Хевисайда

Выводы: Я пришел к выводу что записать  математическую модель сигнала на временных отрезках проще, чем через функции Хевисайда (функция включения).

1.4.2.Представлени сигнала в базисе Функций Уолша

Требуется:

а)определить спектр и построить спектральную диаграмму для заданного ₀ и₀=0.

б)синтезировать сигнал на интервале [0,1] и построить на одном графике заданную и аппроксимированную функцию для ₀=0.

в)рассчитать норму и энергию (на сопротивлении 1Ом)исходного и аппроксимированного сигнала.

г)определить относительную среднеквадратичную ошибку аппроксимации.

Рассмотрим случай для заданного _0.

Опишем наш сигнал и найдем площадь подынтегральной функции B₀

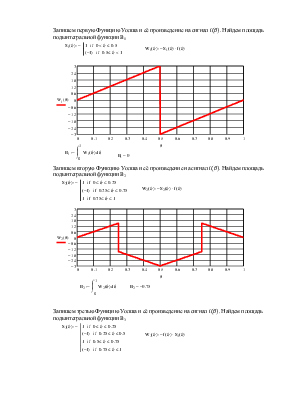
Запишем первую Функцию Уолша и её произведение на сигнал f. Найдем площадь подынтегральной функции B₁

Запишем вторую Функцию Уолша и её произведение на сигнал f. Найдем площадь подынтегральной функции B₂

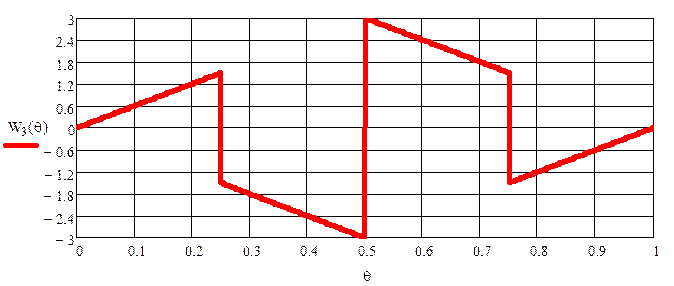
Запишем третью Функцию Уолша и её произведение на сигнал f. Найдем площадь подынтегральной функции B₃

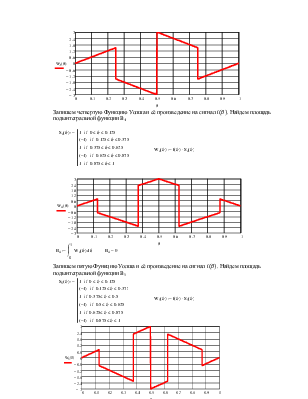
Запишем четвертую Функцию Уолша и её произведение на сигнал f. Найдем площадь подынтегральной функции B₄

Запишем пятую Функцию Уолша и её произведение на сигнал f. Найдем площадь подынтегральной функции B₅

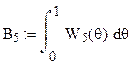
Запишем шестую Функцию Уолша и её произведение на сигнал f. Найдем площадь подынтегральной функции B₆

Запишем седьмую Функцию Уолша и её произведение на сигнал f. Найдем площадь подынтегральной функции B₇

Мы получили следующие значения подынтегральных функций

По найденным коэффициентам B_n осуществляем синтез исходного сигнала

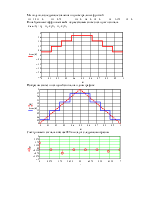
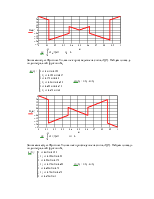
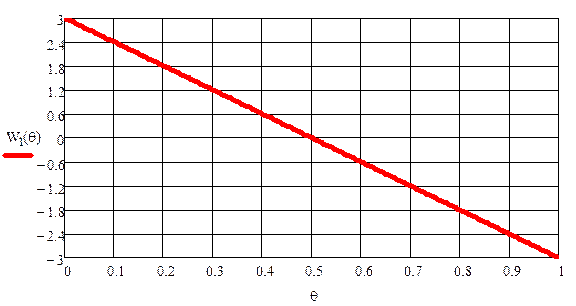
Изобразим синтез и исходный сигнал на одном графике

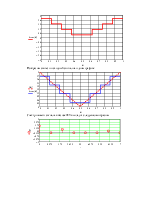
Спектр нашего сигнала в базисе ФУ выглядит следующим образом

Найдем относительную среднеквадратическую ошибку аппроксимации, энергию и норму.

Рассмотрим случай, когда ₀=0.

Опишем наш сигнал и найдем B₀.

Запишем первую Функцию Уолша и её произведение на сигнал f. Найдем площадь подынтегральной функции B₁

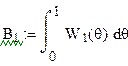
Запишем вторую Функцию Уолша и её произведение на сигнал f. Найдем площадь подынтегральной функции B₂

Запишем третью Функцию Уолша и её произведение на сигнал f. Найдем площадь подынтегральной функции B₃

Запишем четвертую Функцию Уолша и её произведение на сигнал f. Найдем площадь подынтегральной функции B₄

Запишем пятую Функцию Уолша и её произведение на сигнал f. Найдем площадь подынтегральной функции B₅

Запишем шестую Функцию Уолша и её произведение на сигнал f. Найдем площадь подынтегральной функции B₆

Запишем седьмую Функцию Уолша и её произведение на сигнал f. Найдем площадь подынтегральной функции B₇

Мы получили следующие значения подынтегральных функций

По найденным коэффициентам B_n осуществляем синтез исходного сигнала

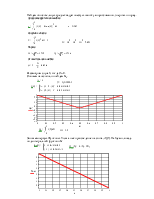
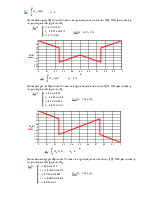
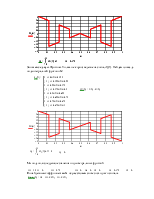
Изобразим синтез и исходный сигнал на одном графике

Спектр нашего сигнала в базисе ФУ выглядит следующим образом

Найдем относительную среднеквадратическую ошибку аппроксимации, энергию и норму.

Вывод: Синтезированный сигнал совпал с исходным, об этом говорят значения среднеквадратичной и относительной ошибок аппроксимации. Норма и энергия исходного и синтезированного сигнала так же  совпадают.

Список литературы:

1.  Гоноровский И.С. Радиотехнические цепи и сигналы: Учебник. – М.: Радио и связь, 1986. - 512 с

2.  Радиотехнические цепи и сигналы. Задачи и задания: Учеб. пособие / Коллектив авторов; под ред. проф. А.Н. Яковлева: Новосибирск, Изд-во НГТУ, 2002. – 348 с. (Серия «Учебники НГТУ»).

3.  Лекции №№ 3-7 Яковлева Альберта Николаевича