Практически, прежде всего, следует убедиться в приемлемости данной аппроксимации. Для этого используют метод приведения к линейному виду. Логарифмируя обе части (1.16), получаем линейную зависимость между логарифмом тока и напряжением:
![]() или
или ![]() . (1.17)
. (1.17)
По заданной ВАХ составляют таблицу, а затем по ней график ![]() или
или ![]() (рис.1.12,а,б).
Если графики мало отличаются от прямой, то ВАХ НЭ можно аппроксимировать
экспонентой. По первому графику значение
(рис.1.12,а,б).
Если графики мало отличаются от прямой, то ВАХ НЭ можно аппроксимировать
экспонентой. По первому графику значение ![]() определяют
как тангенс наклона прямой
определяют
как тангенс наклона прямой ![]() , а по второму – как
среднее значение:
, а по второму – как
среднее значение: ![]() .
.
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
а б Рис.1.12 |
|
 Другой пример.
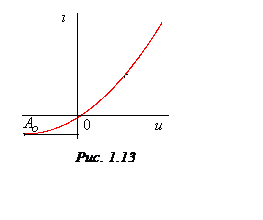
Характеристика полупроводникового диода (рис.1.13) имеет вид:
Другой пример.
Характеристика полупроводникового диода (рис.1.13) имеет вид:
![]() , (1.18)
, (1.18)
где ![]() ,
,![]() выбирают так, чтобы
вся аппроксимированная характеристика лежала выше прямой
выбирают так, чтобы
вся аппроксимированная характеристика лежала выше прямой ![]() , как показано на рис. 1.13. В этом случае
линеаризация производится для функции
, как показано на рис. 1.13. В этом случае
линеаризация производится для функции ![]() , что
возможно, так как величина
, что
возможно, так как величина ![]() .
.
3.3. Кусочно-линейная и кусочно-нелинейная функции.
Реальная плавно изменяющаяся зависимость ![]() заменяется приближенной, состоящей из
отрезков прямых и кривых.
заменяется приближенной, состоящей из
отрезков прямых и кривых.
На рис. 1.14 в качестве примера приведены характеристики, аппроксимированные двумя отрезками: а) прямых линий; б) прямой и параболы.
|
а |
1. 2. |
б |
1. 2. |
|
Рис.1.14 |
|||
Наиболее широкое использование получила кусочно-линейная аппроксимация. Она обеспечивает достаточную точность только при больших амплитудах воздействующих сигналов, а потому применяется при расчетах мощных усилителей, генераторов, умножителей частоты, некоторых схем модуляторов, детекторов и др.
3.4. Трансцендентные функции: гиперболические тангенс и синус, функция Гаусса, тригонометрические функции и др.
В первую очередь следует отметить функцию, содержащую гиперболический тангенс
![]() ,
(1.19)
,
(1.19)
предложенную Н. И. Крыловым, которая хорошо описывает симметричные характеристики и изменения производной (крутизны) и второй производной (кривизны) ряда ВАХ ламп и транзисторов. В тех задачах, где главную роль играет изменения этих параметров, данный вид аппроксимации является незаменимым.
|
|
|
а б
Рис. 1.15
Проанализируем наиболее важные свойства функции ![]() (рис.1.15,а). При малых значениях аргумента c большой точностью
можно считать, что функция равна аргументу, т.е.
(рис.1.15,а). При малых значениях аргумента c большой точностью
можно считать, что функция равна аргументу, т.е.
![]() (при
(при ![]() , ошибка
, ошибка ![]() ),
),
а при больших значениях аргумента – единице, т.е.
![]() (при
(при ![]() , ошибка
, ошибка ![]() ).
).
На рис.1.15, б
приведена ВАХ НЭ, аппроксимированная гиперболическим тангенсом. Здесь ![]() ток насыщения, коэффициенты
ток насыщения, коэффициенты ![]() ,
, ![]() , где
, где ![]() –
крутизна линейного участка характеристики.
–
крутизна линейного участка характеристики.
Тригонометрический синус. Хорошо описывает симметричные характеристики. Для ВАХ, изображенной на рис.1.16 можно записать:
![]() . (1.20)
. (1.20)
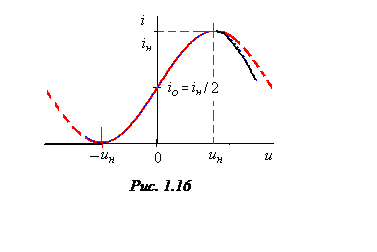
Коэффициенты ![]() можно выразить через
два параметра: ток
можно выразить через
два параметра: ток ![]() в начале координат и начальное
напряжение
в начале координат и начальное
напряжение ![]() . Действительно, при
. Действительно, при ![]() ток равен
ток равен ![]() и
коэффициент
и
коэффициент ![]() . При
. При ![]() ток равен
нулю и, следовательно,
ток равен
нулю и, следовательно, ![]() ,
, ![]() . Отсюда
. Отсюда ![]() ,
, ![]() .
.
Аппроксимация реактивных (индуктивных и емкостных) НЭ ничем не отличается от аппроксимации резистивных НЭ – ламп, транзисторов и др. Используются как упомянутые функции, так и другие. Например, вольт-фарадная характеристика p-n-перехода полупроводникового элемента аппроксимируется выражением:
![]() ,
(1.21)
,
(1.21)
где ![]() – напряжение (обратное) на переходе;
– напряжение (обратное) на переходе; ![]() – высота потенциального барьера
(контактная разность потенциалов);
– высота потенциального барьера
(контактная разность потенциалов); ![]() – емкость перехода при
отсутствии внешнего напряжения (
– емкость перехода при
отсутствии внешнего напряжения (![]() );
); ![]() – постоянная, зависящая от распределения
примесей.
– постоянная, зависящая от распределения
примесей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.