Общие сведения о нелинейных цепях и методах их исследования, страница 3

Для анализа и синтеза линейных цепей разработаны регулярные методы (рис.1.7).

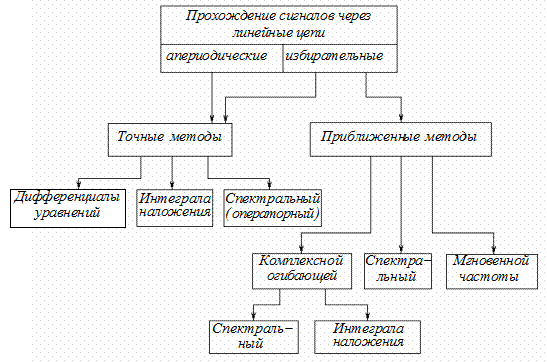
Рис.1.7

По отношению к нелинейным цепям таких регулярных методов нет.  Для исследования этих цепей на основе характеристик НЭ могут использоваться:

– графические методы,

– аналитические методы,

– графо аналитические методы.

Графические методы используются для качественных исследований и для расчета весьма простых цепей при элементарных воздействиях; причем только в тех случаях когда можно удовлетвориться невысокой точностью. Они не обладают общностью, и при каждом изменении параметров цепи или параметров сигнала все построение и расчет приходится выполнять заново.

Аналитические методы. Им присуща общность. При расчете простых цепей и элементарных воздействий они дают более высокую точность. Кроме того, они применимы и при сложных воздействиях. Однако при этом необходимо иметь аналитическое выражение характеристики НЭ. Заводы изготовители НЭ вместе с самими элементами выдают графики характеристик, которые для аналитических расчетов нужно заменять формулами, то есть аппроксимировать.

Графоаналитические методы. Объединяют достоинства предыдущих.

1.3. Аппроксимация характеристик нелинейных элементов

Характеристики нелинейных элементов (НЭ) в большинстве случаев задаются графически (из справочника) или таблично (в ходе эксперимента), поэтому при анализе и расчете схем с НЭ первостепенной стоит задача аппроксимации, т. е. приближенного аналитического представления характеристики НЭ.

Общая задача аппроксимации включает в себя две самостоятельные задачи:

·  выбор класса подходящей функции;

·  определение коэффициентов аппроксимации.

Выбор класса аппроксимирующей функции. Решая эту задачу, необходимо соблюдать требования, в значительной степени противоречивые:

1) простоту функции;

2) достаточную точность (ошибка аппроксимации должна быть одного порядка с разбросом параметров отдельных элементов в партии);

3) наглядность, позволяющую судить об изменении коэффициентов аппроксимации при изменении положения рабочей точки и т. п.;

4) ясность понимания процессов в схеме и выявления свойств схемы, представляющих интерес в конкретном случае.

Выбор  аппроксимирующей функции зависит от:

– характеристики Нелинейного элемента,

– поставленной задачи преобразования сигнала,

– параметров входного сигнала

Например, для выявления и объяснения особенности работы автогенератора, надо аппроксимировать характеристику НЭ полиномом различной степени, вплоть до пятой. Поэтому часто приходится по-разному аппроксимировать одну и ту же характеристику в зависимости от режима работы НЭ, назначения схемы, исследуемых вопросов.

Определение коэффициентов аппроксимации. Оно тесно связано с требуемой точностью. Точность определяется критериями приближения. Обычно применяют критерии равномерного, среднеквадратического и интерполяционного (точечного) приближений. Последний используют наиболее часто. Согласно этому критерию аппроксимируемая функция  и аппроксимирующая функция  (или их производные) должны совпадать в выбранных (заданных) точках с координатами  (рис. 1.8). Число таких исходных точек и, следовательно, уравнений, должно быть равным числу подлежащих определению коэффициентов аппроксимации.

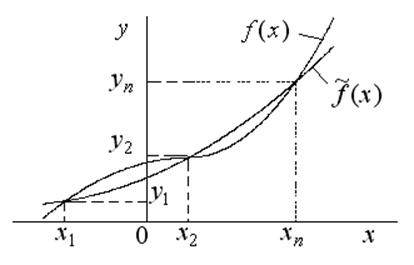
Рис. 1.8

Для определения коэффициентов аппроксимации можно вводить нелинейные масштабы для приведения заданной зависимости к более простому виду, в частности, к линейному. В последнем случае говорят о методе приведения к линейному виду. После нанесения на график экспериментальных точек в новой системе координат, можно легко установить границы линейной области и, следовательно, правомерность использования принятой аппроксимации; коэффициенты находят по этой области графика. Следует отметить, что нелинейные масштабы можно вводить как по каждой переменной, так и по их комбинации (например, произведению).

Если число заданных точек превышает число определяемых коэффициентов аппроксимации, то можно использовать метод наименьших квадратов, при котором среднеквадратическая ошибка минимальна (см. математические справочники).