Общие сведения о нелинейных цепях и методах их исследования

1. ОБЩИЕ СВЕДЕНИЯ О НЕЛИНЕЙНЫХ ЦЕПЯХ

И МЕТОДАХ ИХ ИССЛЕДОВАНИЯ

1.1. Общие сведения о цепях

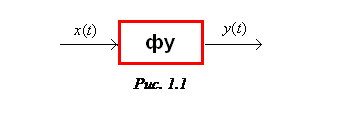На рис.1.1. представлена некоторая цепь в виде функционального узла (преобразователя). На входе преобразователя действует сигнал , который принято называть входным воздействием или входным сигналом. На выходе преобразователя появляется сигнал , являющийся откликом (реакцией) на входное воздействие. Отклик зависит как от вида входного воздействия, так и от свойств цепи. На этом основании выходной сигнал  можно записать в форме причинно-следственной связи:

= ,                                                          (1.1)

где символами  обозначены параметры элементов цепи.

Радиотехническая цепь, таким образом, выполняет функции некоторого оператора, преобразующего сигнал одного вида в другой. Функциональная зависимость (1.1) определяется свойствами сигнала и свойствами цепи. Свойства у различных цепей различны и являются удобными признаками для классификации цепей.

Первым признаком, по которому подразделяют цепи, является вопрос о применимости принципа суперпозиции (принципа независимости действия внешних сил). По этому признаку все цепи целесообразно делить на линейные и нелинейные.

          Линейными называются цепи (преобразователи), для которых справедливы равенства:

;   .                    (1.2)

Первое равенство выражает свойство аддитивности, второе – однородности. Свойство аддитивности отражает принцип суперпозиции, который формулируется так: реакция цепи на сумму воздействий равна сумме реакций на каждое воздействие в отдельности.

Вторым признаком, по которому удобно классифицировать цепи и системы, является вопрос о возникновении в результате преобразования сигнала колебаний новых частот, то есть о возможности трансформации  частотного спектра. В линейных цепях с постоянными параметрами не возникают колебания новых частот, не содержащихся во входном сигнале. Объясняется это тем, что дифференцирование и интегрирование гармонических колебаний (только эти операции совершаются в линейных цепях) не меняет их формы, а следовательно, и спектра частот сигнала.

По этим признакам все цепи целесообразно делить на группы.

1. Линейные цепи. Их часто называют: линейные стационарные цепи, Линейные цепи с постоянными параметрами или линейные инвариантные к сдвигу цепи (ЛИС-цепи). Для краткости их будем называть просто линейными цепями. Параметры  в формуле (1.1) – величины постоянные, не зависящие ни от электрического режима, ни от времени. К ним применим принцип суперпозиции (наложения), а трансформация спектра невозможна.

2. Параметрические или линейные нестационарные цепи. Параметры не зависят от электрического режима, но зависят (все или один) от текущего времени , например:

Параметрическую цепь в отличие от линейной (и нелинейной) следует изображать в виде цепи, находящейся под двумя воздействиями (рис.1.2): входного сигнала  и управляющего сигнала . Связь между  и  – линейная, но так как она выражается через параметры, зависящие от , спектр сигнала на выходе отличается от спектра входного сигнала. Сущность сказанного поясняется рис.1.3: у линейной цепи угол наклона прямой  является постоянным, а у параметрической цепи – функцией времени.

Простейшая параметрическая цепь представляет собой активное сопротивление, изменяющееся во времени по периодическому закону. Рассматривая для удобства в качестве изменяемого параметра проводимость (крутизну) , можно записать для тока следующее выражение:

,                                      (1.3)

где - переменная крутизна линейной ВАХ (рис.1.3, где , а ).

Пусть напряжения и крутизна изменяются в простейшем случае по гармоническому закону:

,  .                      (1.4)

Подставляя (1.4) в (1.3) , после элементарных преобразований получим:

 +

+ .

Очевидно, что в спектре тока присутствует не только составляющая с частотой входного сигнала , но составляющие с суммарной  и разностной  частотами. Это позволяет использовать параметрические цепи для переноса спектра частоты  на величину  вправо и влево по оси частот  (преобразование частоты, амплитудная модуляция, синхронное детектирование амплитудно-модулированных сигналов).

3. Нелинейные стационарные цепи. Параметры  (или один из них) зависят от электрического режима цепи, то есть от тока или напряжения. Следствием этого является нелинейноcnm функциональной зависимости (1.1), которая в частных случаях может иметь, например, вид: , или .

4. Нелинейные нестационарные (нелинейно-параметрические) цепи, параметры которых в отличие от нелинейных цепей меняются ещё и во времени.

Строго говоря, все цепи следует считать нелинейно-параметрическими, так как все причинно-следственные связи являются нелинейными и меняются во времени. Однако, при определенных условиях изучение цепей можно и следует вести дифференцированно.

Все простейшие радиотехнические цепи составляются из трех элементов: резисторов, конденсаторов и катушек индуктивности. Каждый из элементов характеризуется своим параметром: резисторы – сопротивлением (или проводимостью ), конденсаторы – емкостью , катушки – индуктивностью .

В зависимости от способности элементов рассеивать или запасать энергию их можно разделить на:

– диссипативные, не обладающие способностью сохранять энергию, она в них необратимо превращается в тепло;

– консервативные, сохраняющие (консервирующие) энергию. К ним относятся конденсаторы и катушки индуктивности, запасающие соответственно электрическую и магнитную энергию. Элементы этой группы называются реактивными.