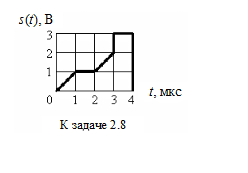Сборник задач для индивидуальных занятий студентов. Ч.1, страница 4

2.8. Полезный сигнал изображен на рисунке. Приведите схему оптимального приемника обнаружения Котельникова и укажите ее основные параметры.

2.9. Амплитуда сигнала с полностью известными параметрами увеличилась в два раза. Какие изменения необходимо внести в приемник обнаружения, работающий по критерию Котельникова, если р₀ = р₁ = 0,5?

2.10. Определить графически относительный порог в когерентном приемнике обнаружения (демодуляторе) бинарных сигналов (информационных битов), работающем по критерию минимума средней вероятности ошибок для двух случаев: а) р₀ = р₁ = 0,5, б) р₀ = 0,3, р₁ = 0,7 при ОСШ q² = 25. Пояснить влияние априорных вероятностей на величину порога.

2.11. Привести схему оптимального обнаружителя пачки из четырех когерентных радиоимпульсов. Их начальные фазы: j₁ – неизвестна, j₂ – j₁ = 30°, j₃ – j₂ = 40°, j₄ – j₃ = 50°.

2.12. Вероятности превышения порога бинарного квантования в цифровом обнаружителе пачки из трех импульсов F₁ = 0,1, D₁ = 0,6. Каковы значения вероятностей ложной тревоги р_лт и правильного обнаружения р_по при цифровом пороге k = 2? Как изменятся р_лт и р_по при уменьшении k до 1?

2.13. Определить вероятность ложной тревоги при цифровом обнаружении пачки из четырех радиоимпульсов, если отсчеты помехи на входе бинарного квантователя подчиняются экспоненциальному распределению , порог бинарного квантования u₀ = 4, а цифровой порог k = 3.

2.14. Определить графически относительный порог в некогерентном приемнике обнаружения (демодуляторе) бинарных сигналов (информационных битов), работающем по критерию минимума средней вероятности ошибок для двух случаев: а) р₀ = р₁ = 0,5, б) р₀ = 0,3, р₁ = 0,7 при ОСШ q² = 25. Пояснить влияние априорных вероятностей на величину порога.

2.15. По цифровому когерентному каналу связи передается двоичная информация (поток битов) со скоростью 2500 бит/с методом амплитудной телеграфии. Принято решение повысить скорость передачи на 25 %. Изменением какого параметра радиосигнала (и насколько) это достигается? Как это изменение сигнала повлияет на среднюю вероятность ошибок? Каким образом можно восстановить ее прежнее значение?

2.16. При обнаружении флюктуирующих радиосигналов распределение дискретной выборки, взятой на выходе амплитудного детектора, подчинено закону Рэлея:

причем D₀ – дисперсия шума приемника на входе детектора, а D₁ = D₀ + + D_c, где D_c – дисперсия сигнала. Синтезировать алгоритм последетекторного обнаружения пачки из n импульсов, основанный на принципе максимального правдоподобия.

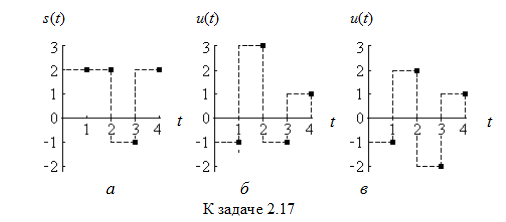
2.17. На вход оптимального обнаружителя дискретного сигнала s(t) (см. рисунок а) на фоне дискретного белого гауссовского шума последовательно поступают две реализации колебаний u(t), показанные на рисyнках б и в. Какое решение в каждом из этих двух случаев вынесет обнаружитель, работающий по критерию максимального правдоподобия?

2.18. В таблице представлены данные на входе обнаружителя дискретного сигнала s(i) = 2, , при его наблюдении на фоне некоррелированного гауссовского шума с нулевым средним значением и единичной дисперсией. Найти зависимость принятого решения от стоимости ошибок  при , если р₀ = р₁. Решить также задачу при р₀ = 0,75 и сопоставить полученные результаты.

2.19. СПМ помехи – белого шума, выделяемая на сопротивлении 1 Ом, составляет 10^–18 Вт/Гц. Какую амплитуду должен иметь радиоимпульс с прямоугольной огибающей длительностью 1 мкс, чтобы при его обнаружении вероятности ложной тревоги и правильного обнаружения составили  В и 0,95 соответственно? Начальная фаза высокочастотного заполнения известна. Задачу решить также для случая, когда начальная фаза высокочастотного сигнала – случайная величина. Сопоставить результаты.

2.20. Амплитуда радиоимпульса с прямоугольной огибающей равна  В, его длительность 10 мкс. Определить допустимый уровень СПМ помехи – белого шума, выделяемой на сопротивлении 1 Ом, при котором обнаружение сигнала характеризуется вероятностями ложной тревоги  и правильного обнаружения 0,9. Начальная фаза сигнала в приемнике известна. Решить задачу также при случайной начальной фазе радиосигнала. Сравнить полученные результаты.