Сборник задач для индивидуальных занятий студентов. Ч.2, страница 4

2.90.  Определить горизонтальный размер приемопередающей антенны РЛС кругового обзора, если отношение сигнал/шум для всей пачки q² = 10, рабочая частота 10 ГГц, а допустимая среднеквадратичная ошибка измерения азимута составляет 0,15º. В системе используется цифровой съем угловой координаты, в результате которого выполняется представление данных в виде 10-разрядного двоичного кода.

2.91.  РЛС обнаруживает цель на расстоянии 300 км. Длительность зондирующих импульсов 3 мкс, форма – гауссова, отношение сигнал/шум 23 дБ. Выходным устройством является преобразователь дальности в двоичный код. Частота следования эталонных импульсов преобразователя 5 МГц. Определить полную среднеквадратичную ошибку измерения дальности.

2.92.  Прямоугольный импульс, имеющий амплитуду 0,5 мв и длительность 200 мкс, принимается на фоне белого шума, выделяющего на сопротивлении 1 Ом мощность 2 мкВт в полосе частот 1 МГц. Какова минимальная среднеквадратичная погрешность измерения радиальной скорости объекта с помощью такого сигнала, если его несущая частота равна 1 ГГц?

2.93.  На вход измерителя неизвестного постоянного параметра s поступает дискретная выборка . Здесь ε_i – гауссовская помеха с независимыми значениями, имеющая нулевое математическое ожидание и дисперсию D. Найти алгоритм оценки максимального правдоподобия и выражение для дисперсии ошибок полученной оценки. Найти также нижнюю границу ошибок, определяемую неравенством Крамера–Рао, сравнить ее с дисперсией полученной оценки и сделать вывод об ее эффективности.

2.94.   Дискретная независимая выборка , принадлежит экспоненциальному распределению 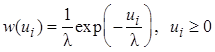, содержащему неизвестный параметр . Определить значение  оценки максимального правдоподобия, найти смещение и дисперсию этой оценки. Сопоставить дисперсию с нижней границей, определяемой неравенством Крамера–Рао, и сделать вывод об эффективности оценки.

2.95.   Азимут маневрирующей цели описывается стохастическим разностным уравнением  где i = 1, 2, 3, … – дискретное время; – информационный гауссовский белый шум, имеющий нулевое среднее значение и дисперсию . В результате работы пеленгатора формируются первичные измерения  содержащие некоррелированный шум измерений n_i с дисперсией D_n = (30′)² и нулевым средним. Записать алгоритм фильтра Калмана, выполняющего вторичную обработку (сглаживание) измерений. Определить дисперсию сглаженных оценок и найти выигрыш, обусловленный сглаживанием, как в динамике, так и в установившемся состоянии.

2.96.   Для передачи информации используется амплитудно-импульсная модуляция, при которой амплитуды импульсов-переносчиков, следующих с периодом с, изменяются в соответствии с мгновенными значениями сообщения. Последнее описывается стохастическим разностным уравнением

, где i – дискретное время (номер импульса); – информационный белый шум (), – дисперсия сообщения; – коэффициент корреляции соседних значений. Наблюдаемый в приемнике сигнал искажен белым шумом наблюдения  ). При приеме используется дискретный фильтр Калмана. Записать его алгоритм. Определить, при каком значении коэффициента  установившаяся дисперсия фильтрации составит 1 % от мощности сообщения. Какой частотой полосе непрерывного сообщения , из которого образованы отсчеты , соответствует найденное значение ?

2.97.  При вторичной обработке радиолокационной информации измеряется траектория цели, дальность которой изменяется по закону , где i = 0, 1, 2,… – номер измерения; T = 1 с – период, с которым образуются первичные измерения . Шум первичных измерений  независим и распределен по нормальному закону с параметрами  м. Найти алгоритм получения оценок максимального правдоподобия для параметров R₀ по выборке первичных данных . Определить значения оценок для исходных данных, представленных в таблице. Определить дисперсии оценок.