Сборник задач для индивидуальных занятий студентов. Ч.2

Различение сигналов

2.55. Используемые в СПИ дискретные сигналы описываются функциями . Сигнал на входе различителя , где k – неизвестный при приеме номер сигнала, а n(i) – помеха с независимыми значениями и нормальным распределением, имеющая нулевое математическое ожидание и единичную дисперсию. Поступивший дискретный сигнал представлен следующей таблицей.

Какое решение будет вынесено байесовским различителем, если априорные вероятности p₀ = 1/2, р₁ = 1/8, а стоимости всех ошибок одинаковы?

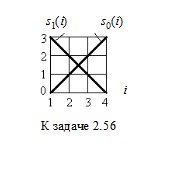2.56. Различитель, предназначенный для приема дискретных сигналов  и , изображенных на рисунке в виде огибающих, работает по критерию Байеса. Стоимости ошибок П₀₁ = 1, П₁₀ = 2, априорные вероятности р₀ = 2/3, р₁ = 1/3. Аддитивная некоррелированная гауссовская помеха имеет нулевое среднее значение и единичную дисперсию. Поступивший на вход различителя сигнал представлен таблицей. Какое решение вынесет различитель? Каким будет решение, если П₀₁ = 1, П₁₀ = = 100? Объясните результаты.

2.57. При различении дискретных сигналов  и , поступившие данные  заданы в виде таблицы. Помеха n(i) – гауссовский некоррелированный шум с нулевым средним значением и единичной дисперсией. Стоимости ошибок П₀₁ = П₁₀.

Найти зависимость принятого решения от априорной вероятности р₀ сигнала  при изменении последней от 0 до 1. Решить задачу также при П₀₁ = 2 П₁₀. Сделать качественный анализ результатов.

2.58. Определите, являются ли сигналы  и  ортогональными на интервале  в следующих случаях: а)  и ; б)  и ; в)  и .

2.59. Определите, являются ли сигналы  и  ортогональными на интервале  в следующих случаях: а)  и ; б)   и  ;  в)  и .

2.60. Покажите, что три функции, приведенные на рисунке, попарно ортогональны на интервале (–2, 2).

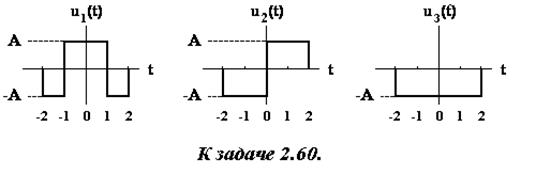
Определите значение константы А, преобразующей данный набор в набор ортонормированных функций. Выразите сигнал x(t):

через полученные ортонормированные функции.  

2.61. Даны следующие функции:  и . Определите константу A, при которой эти функции ортогональны на интервале .

2.62. Биполярный двоичный сигнал  – это импульс +1 В или –1 В на интервале (0, T). К сигналу добавляется аддитивный белый гауссовский шум с двухсторонней СПМ 10^–3 Вт/Гц. Определите максимальную скорость передачи битов, которую можно поддерживать при вероятности появления ошибочного бита Р_ош £ 10^–3.

2.63. Двоичные данные передаются при помощи биполярных импульсов, амплитудные значения которых на выходе согласованного фильтра равны +1 В или –1 В. Дисперсия гауссовского шума на его выходе 0,1 В². Определите оптимальный порог различения (дающий минимальную вероятность ошибки) при следующих априорных вероятностях: а) р₁ = 0,5, б) р₁ = 0,7; в)р₁ = 0,2. Объясните влияние априорных вероятностей на величину порога.

2.64. В приемнике различения, осуществляющем прием двоичных данных, решение принимается сравнением с порогом данных . Здесь сигнал принимает значения а₁ = 1 В, а₂ = –1 В, а шум n₀ имеет равномерное распределение. Плотности условного распределения даются выражениями

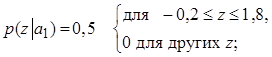
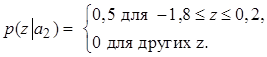
Определите вероятность появления ошибки для равновероятной передачи символов и использования оптимального порога принятия решения, минимизирующего среднюю вероятность ошибок.

2.65. Оптимальный приемник решает задачу различения двух сигналов  наблюдаемых на фоне белого шума с СПМ 10^–17 Вт/Гц. Какую амплитуду S₀ должны иметь сигналы для достижения вероятности ошибок различения 10^–3, если длительность элементарной посылки составляет 10^–3с, а начальные фазы имеют значения: а) ; б)

2.66. В системе передачи информации, использующей 32 сигнала вида  требуется обеспечить вероятность ошибок не выше 10^–4. При какой амплитуде S₀ достигается этот показатель, если прием выполняется на фоне белого шума, имеющего СПМ 10^–18 Вт/Гц?

2.67. Для передачи дискретной информации используются ортогональные полиномы Лежандра:

Определить амплитудные множители S₀, S₁, S₂, при которых эти сигналы имеют равные энергии, а вероятность ошибок при приеме не превысит 10^–3. Длительность элементарной посылки 2T = 10^–3 с, символы равновероятны, помеха – белый шум с СПМ 10^–18 Вт/Гц.

2.68. Определить энергетический проигрыш при различении М ортогональных детерминированных сигналов по сравнению с различением М симплексных сигналов, если М = 2, 3, 4, 5, 10, 100.