Министерство образования Российской Федерации
НГТУ
Кафедра РП и РПУ
Расчетно-графическое задание
по радиоавтоматике
Вариант №12
Студент: Есауленко К.Е.
Группа: РТ5-91
Преподаватель: Лявданский С.Е.
Новосибирск 2012
Задание на работу
1) По имеющейся в исходных данных передаточной функции разомкнутой системы записать передаточную функцию замкнутой системы.
2) Записать передаточную функцию для ошибки от регулирующего воздействия.
3) Изобразить структурную схему исследуемой системы, считая систему следящей.
4) Записать характеристические полиномы разомкнутой и замкнутой системы.
5) Исследовать систему на устойчивость по критерию Гурвица.
6) Исследовать систему на устойчивость по критерию Михайлова методом чередующихся корней.
7) Исследовать систему на устойчивость по критерию Михайлова с указанием масштабов по обеим осям.
8) Исследовать систему на устойчивость по критерию Найквиста.
9) Построить годограф Найквиста с указанием масштабов по обеим осям.
10) Определить запас устойчивости по модулю и по фазе.
11) Вычислить коэффициенты ошибки и найти ошибку
регулирования системы в установившемся режиме ![]() при заданной входной функции.
при заданной входной функции.
12) Построить график ![]() в масштабе по обеим осям.
в масштабе по обеим осям.
Входное воздействие для всех вариантов в общем виде записывается функцией:
![]()
Исходные данные:
Структура системы: 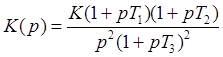 , где
, где ![]()
Выполнение:
1) Находим передаточную функцию замкнутой системы по исходной разомкнутой.
Передаточная функция замкнутой системы имеет вид:
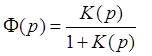 (1)
(1)
Подставляя выражение исходной передаточной функции разомкнутой системы в выражение (1), получаем
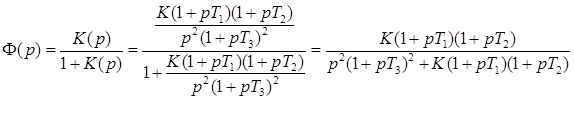
2) Найдем передаточную функцию ошибки.
Пользуясь выражением 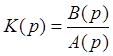 , мы можем найти передаточную функцию ошибки:
, мы можем найти передаточную функцию ошибки:
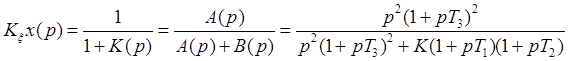
3) Структурная схема исследуемой системы.
Для того, чтобы нарисовать структурную схему, нужно разложить выражение исходной передаточной функции на составляющие.
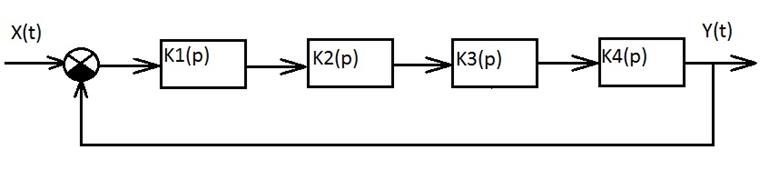
Здесь 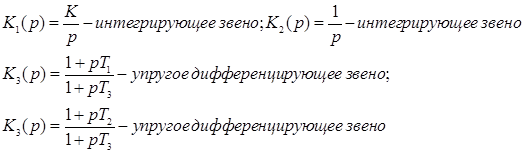
4) Запишем характеристические полиномы разомкнутой и замкнутой системы.
1.Разомкнутая система.
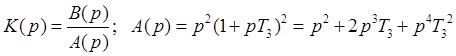
Коэффициенты характеристического полинома:
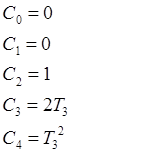
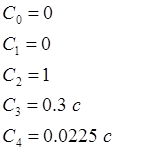
2. Замкнутая система.
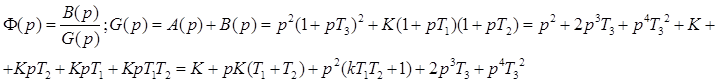
Коэффициенты характеристического полинома:
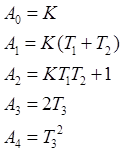
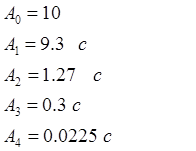
5) Исследуем систему на устойчивость по критерию Гурвица.
По критерию Гурвица существуют два условия; необходимое и достаточное.
Необходимым условием устойчивости является положительность коэффициентов
Как видно необходимое условие выполняется. Перейдем к достаточному условию.
Достаточное условие – это положительность всех диагональных определителей матрицы Гурвица. Эта матрица составляется из коэффициентов An.
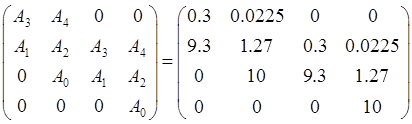
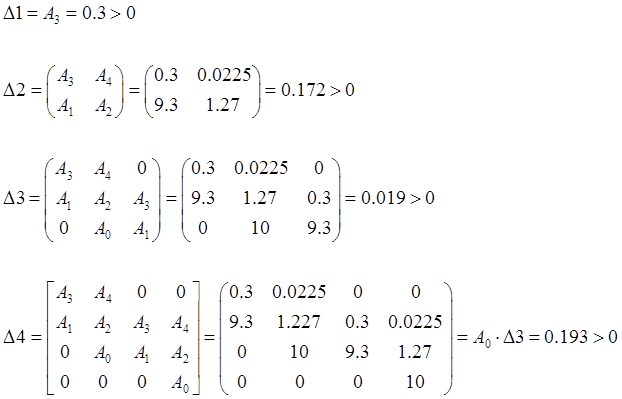
Достаточное условие критерия Гурвица выполняется, следовательно система устойчива.
6) Исследование системы по критерию Михайлова, методом чередующихся корней.
Передаточная функция замкнутой системы:
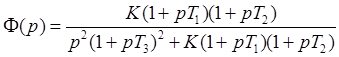
Характеристический полином:
![]()
Перейдем в частотную область:
![]()
Запишем коэффициенты:
![]()
Найдем частоты пересечения мнимой оси, для чего приравняем к нулю вещественную часть и найдем корни полученного уравнения.
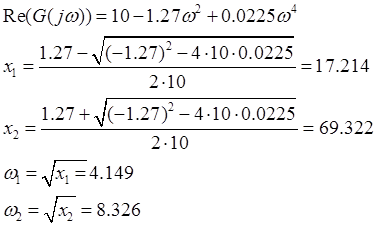
Находим частоты пересечения вещественной оси:
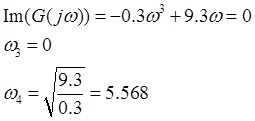 Расположим все четыре частоты пересечения осей
по порядку их возрастания и подчеркнем корни одного уравнения сплошной чертой,
а другого – волнистой.
Расположим все четыре частоты пересечения осей
по порядку их возрастания и подчеркнем корни одного уравнения сплошной чертой,
а другого – волнистой.
0 4.149 5.568 8.326
Корни чередуются. Правило чередующихся корней выполняется, следовательно, система устойчива.
7) Исследовать систему на устойчивость по критерию Михайлова.
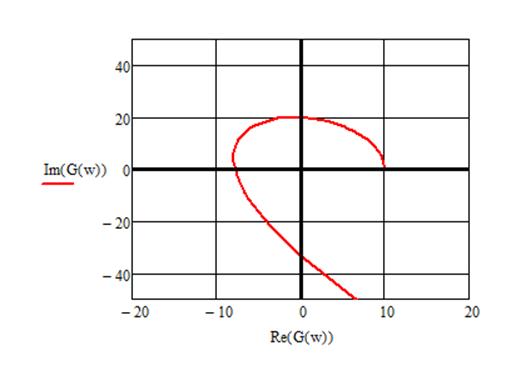
8) Исследовать систему на устойчивость по критерию Найквиста.
Имеется 4 последовательно включенных звена: 2 интегрирующих и 2 упруго интегрирующих.
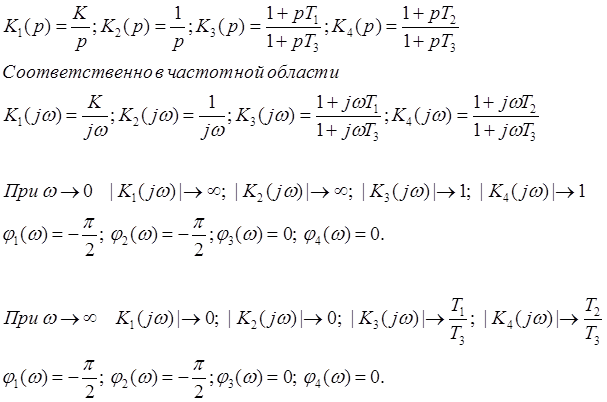
Т.к. звенья соединены последовательно, то можно записать
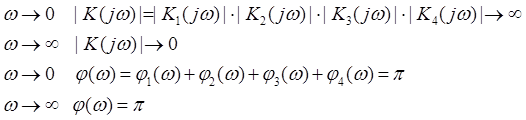
На основании проведенного анализа можно построить годограф Найквиста
9) Построить годограф Найквиста с указанием масштабов по обеим осям.
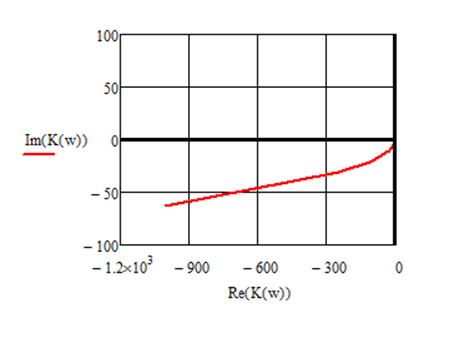
Построим годограф Найквиста в
увеличенном масштабе и найдем запас устойчивости по модулю.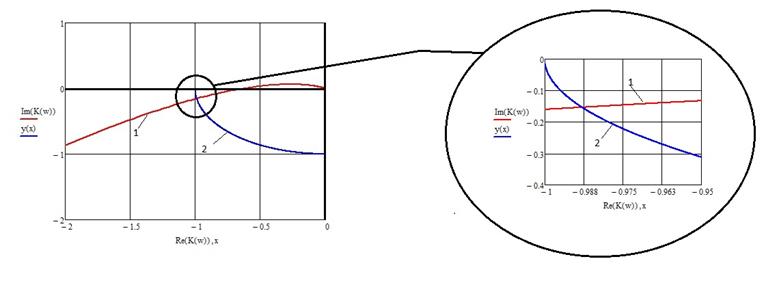
Здесь 1-годограф Найквиста, 2-окружность единичного радиуса.
Как видим, годограф не пересекает точку (-1;0), следовательно, система устойчива.
10) Определить запас устойчивости по модулю и по фазе.
Запас устойчивости по модулю
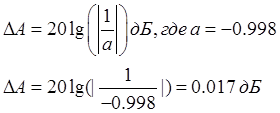
Запас устойчивости по фазе составляет 90 градусов.
11)
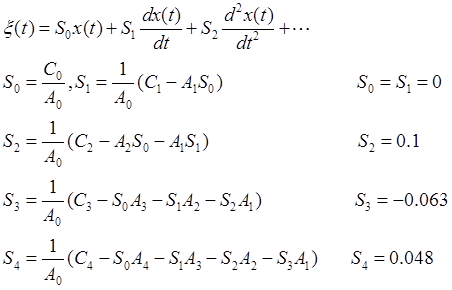 |
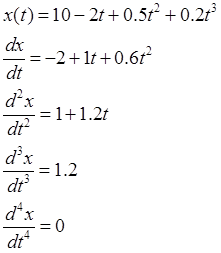
Получим выражение для ошибки регулирования
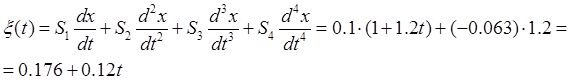
12) Построить график ![]() в масштабе по обеим осям.
в масштабе по обеим осям.
|
|
Список литературы:
1) Радиоавтоматика. Методические указания к выполнению расчетно-графического задания для студентов 3 курса факультета РЭФ специальностей 210405 и 210300. Лявданский С.Е. Новосибирск 2010.
2) Конспект лекций.
3) Радиоавтоматика. Методические указания к самостоятельной аудиторной работе (САР) для студентов 3 курса РТФ специальности 2301 всех форм обучения. Лявданский С.Е. Новосибирск 1990.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.