Министерство образования
Российской Федерации
УНИВЕРСИТЕТ
Расчётно-графическое задание № 1
“Теория управления радиоавтоматикой”
Выполнил:
Студент: Поречный Д.Н.
Группа: РТ5-24
Проверил:
Преподаватель: Лявданский С.Е.
Новосибирск 2005
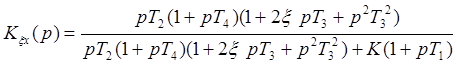 |
Задание:
1. Записать передаточную функцию разомкнутой системы К(р)
2. Зарисовать структурную схему системы считая ее следящей.
Перечислить все типовые звенья в системе
3. Записать передаточную функцию и дифференциальное
уравнение замкнутой системы.
4. Записать передаточную функцию для ошибки от регулирующего
воздействия.
5. Записать характеристические полиномы разомкнутой и замкнутой схемы
и вычислить коэффициенты.
6. Произвести анализ устойчивости по критерию Гурвица.
7. Произвести анализ устойчивости по критерию Михайлова (метод
чередующихся корней). Построить годограф Михайлова.
8. Произвести анализ устойчивости по критерию Найквиста. Построить
годограф Найквиста.
9. Определить ошибку регулированияи построить график.
1. Записать передаточную функцию разомкнутой системы K(p).
Выразим передаточную функцию разомкнутой системы через передаточную функцию ошибки от регулирующего воздействия
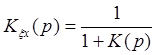 |
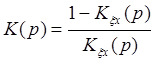
Следовательно передаточная функция разомкнутой системы будет выглядеть так:
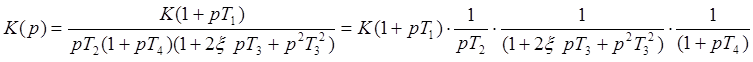 |
2) Зарисовать структурную схему системы считая ее следящей, перечислить все типовые звенья в системе.
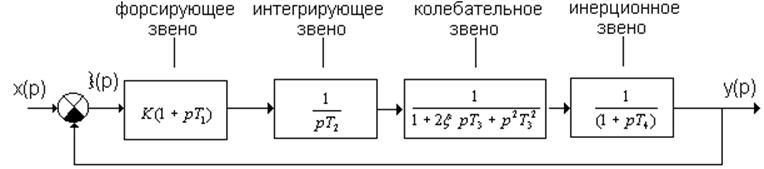 |
Рис.1.
3. Записать передаточную функцию и дифференциальное уравнение замкнутой системы.
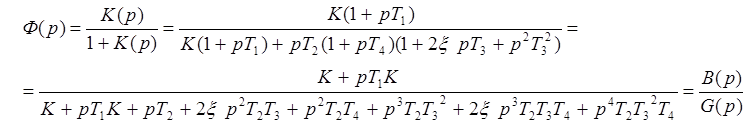 |
b0 =K b0 = 15 a0 =K a0 = 15
b1 =![]() b1 = 19.5
a1 = (
b1 = 19.5
a1 = (![]() +
+![]() )
a1 = 29.5
)
a1 = 29.5
a2 =![]() a2 = 12
a2 = 12
a3 = ![]() a3 =
2.1
a3 =
2.1
a4 = ![]() a4 = 0.1
a4 = 0.1
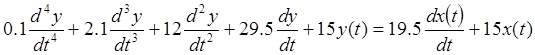
4. Записать передаточную функцию для ошибки от регулирующего воздействия.
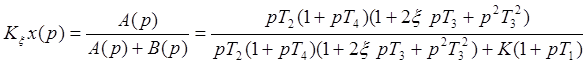 |
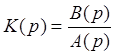 |
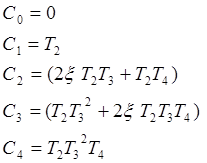 |
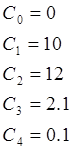 |
||
Характеристический полином замкнутой системы
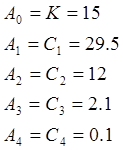 |
6. Произвести анализ устойчивости по критерию Гурвица.
По критерию Гурвица существуют два условия; необходимое и достаточное.
Необходимым условием устойчивости является положительность коэффициентов
Как видно необходимое условие выполняется. Перейдем к достаточному условию.
Достаточное условие – это положительность всех диагональных определителей матрицы Гурвица. Эта матрица составляется из коэффициентов An.
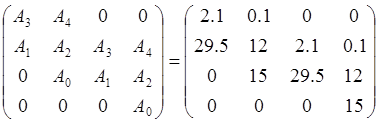 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Достаточное условие критерия Гурвица выполняется, следовательно, система устойчива.
7. Произвести анализ устойчивости по критерию Михайлова (метод
чередующихся корней). Построить годограф Михайлова.
По
критерию Михайлова, система n – порядка будет устойчива, если годограф
характеристической частотной функции ![]() в диапазоне частот от
нуля до бесконечности последовательно против часовой стрелки обходит n
квадрантов комплексной плоскости. Т.е. если система устойчива, то годограф
функции
в диапазоне частот от
нуля до бесконечности последовательно против часовой стрелки обходит n
квадрантов комплексной плоскости. Т.е. если система устойчива, то годограф
функции ![]() поочередно пересекает вещественную и
мнимую оси и не может подряд два раза пересечь одну и ту же ось.
поочередно пересекает вещественную и
мнимую оси и не может подряд два раза пересечь одну и ту же ось.
Передаточная функция
замкнутой системы: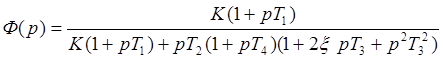
Характеристический полином:
![]()
Перейдем в частотную область:
![]()
Запишем коэффициенты:
![]()
![]()
![]()
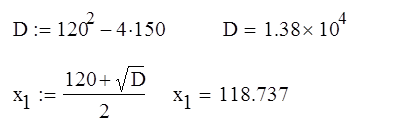
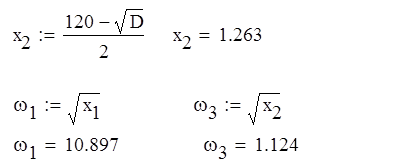
Находим частоты пересечения вещественной оси:
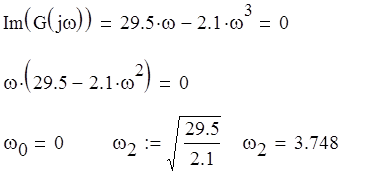
![]() w = 0 G(jw) = 15
w = 0 G(jw) = 15
w = 1.124 G(jw) = 30,176j
w = 3.748 G(jw) = -133.837
w = 10.897 G(jw) = - 2396j
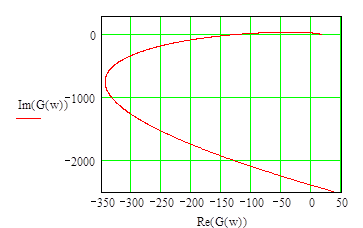
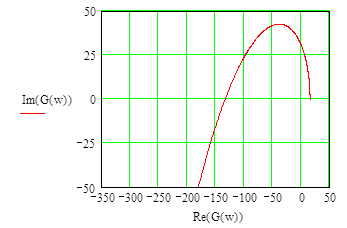
Рис 2. Рис 3.
Система устойчива, так как оси пересекаются по порядку.
8. Произвести анализ устойчивости по критерию Найквиста. Построить
годограф Найквиста. Определить запас устойчивости системы по модулю и по
фазе.
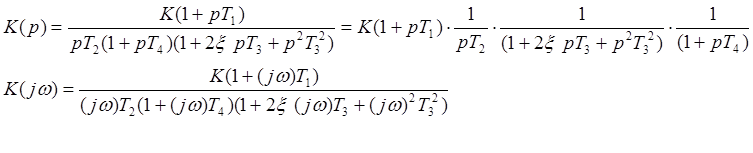 |
Используя полученные данные построим годограф:
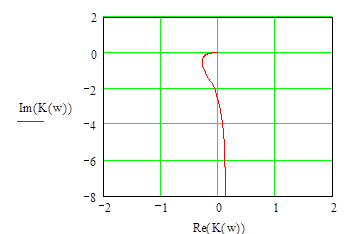
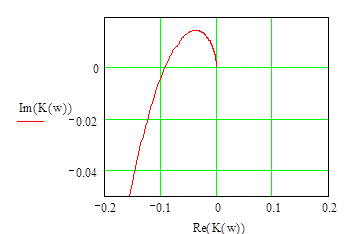
рис. 4 рис. 5
Годограф системы не охватывает точку «-1», следовательно, система устойчива.
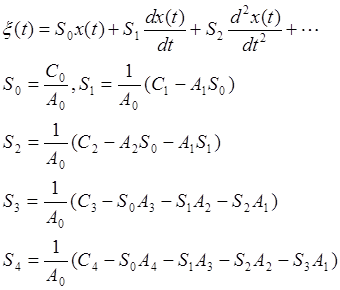 |
Cn – коэффициенты полинома А(р) – характеристический полином разомкнутой системы
An – коэффициенты полинома G(p) – характеристический полином замкнутой системы.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
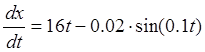
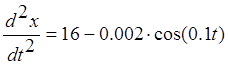
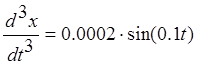
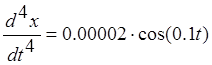
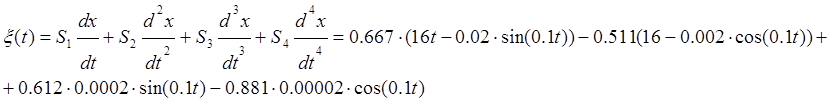
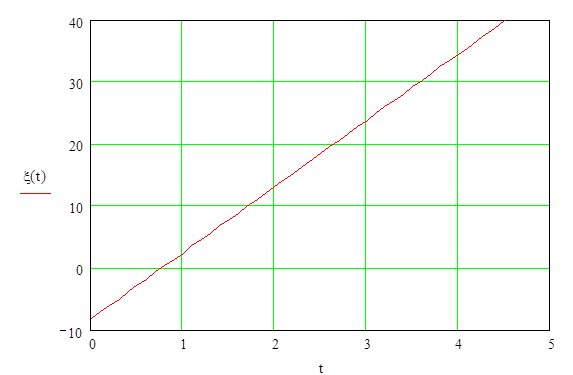
Рис.4.
Список использованной литературы:
1) «Радиоавтоматика методические указания», №1258: 621.39 Р154, –Нск., 1995.
2) «Радиоавтоматика методические указания к самостоятельной аудиторной работе», №345: 621.39 Р154, -Нск, 1990.
3) Конспект лекций по курсу «Теория управления радиоавтоматикой».
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.